
【题目】某校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下频率分布表.根据相关信息回答下列问题:
(1)求a,b的值,并画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数在[60,80)内学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人的分数在[70,80)内的概率.
【答案】
(1)解:a=6,b=0.25
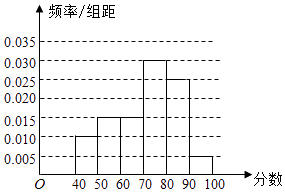
(2)解:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
(3)解:由题意知[60,70)中抽2人,[70,80)中抽取4人,则任取两人共有 ![]() =15种取法(10分)
=15种取法(10分)
至多有一人在[70,80)总有9种情况 ![]() …(12分)
…(12分)
答:分数在[70,80)内的频率为0.3,本次考试的平均分为71,至多有1人的分数在[70,80)内的概率为 ![]()
【解析】(1)求得a,b的值,再画出频率分布直方图;(2)常用组区间的中点值代表该组数据,再估计本次考试的平均分数;(3)先求出基本事件的个数,再利用古典概型的概率求得所给事件的概率.
【考点精析】本题主要考查了分层抽样的相关知识点,需要掌握先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本才能正确解答此题.


科目:高中数学 来源: 题型:
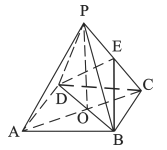
【题目】如图,正四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 是正方形的中心,
是正方形的中心, ![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(I)证明: ![]() 平面
平面![]() ;
;
(II)证明:平面![]() 平面
平面![]() ;
;
(III)已知: ![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为1的正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,当一个圆为正方形内切圆时半径最大,另一圆半径最小,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数。
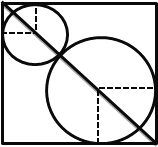
求:(1)函数![]() 的解析式;
的解析式;
(2)![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 在线段
在线段![]() 上,
上, ![]() ,
, ![]() .
.
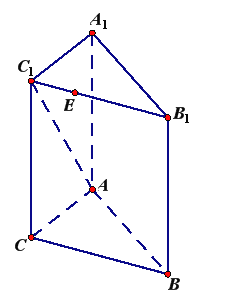
(1)求证: ![]() ;
;
(2)试探究:在![]() 上是否存在点
上是否存在点![]() ,满足
,满足![]() 平面
平面![]() ,若存在,请指出点
,若存在,请指出点![]() 的位置,并给出证明;若不存在,说明理由.
的位置,并给出证明;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速![]() (单位:
(单位: ![]() )与其耗氧量单位数
)与其耗氧量单位数![]() 之间的关系可以表示为函数
之间的关系可以表示为函数![]() ,其中
,其中![]() 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为![]() 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.
(1)求出游速![]() 与其耗氧量单位数
与其耗氧量单位数![]() 之间的函数解析式;
之间的函数解析式;
(2)求当一条鲑鱼的游速不高于![]() 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是C: ![]() +
+ ![]() =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com