练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求下列函数的最小正周期

    (1)y＝tan－；

    (2)y＝2|sin(4x－)|；

    (3)y＝(asin＋cosx)2(a∈R)；

    (4)y＝2cosxsin(x＋)－sin2x＋sinxcosx

    答案：
    解析：

    		 　　解答　　(1)因为y＝tan －

    　　解答　　(1)因为y＝tan－

    　　＝－＝－＝－cotx

    　　所以此函数的最小正周期为π．

    　　(2)注意到y＝sin(4x－)的最小正周期T＝＝，结合y＝2|sin(4x－)|的图象，知其最小正周期为×＝．

    　　(3)因为y＝[sin(x＋)]2

    　　＝(a2＋1)sin2(x＋)

    　　＝(a2＋1)·(为辅助角)．

    　　所以此函数的最小正周期为＝π

    　　(4)因为y＝2cosx(sinx＋cosx)－sin2x＋sinxcosx

    　　＝sinxcosx＋cos2x－sin2x＋sinxcosx

    　　＝sin2x＋cos2x＝2sin(2x＋)，

    　　所以该函数的最小正周期是T＝＝π．

    　　评析　　求三角函数最小正周期的基本方法有两种：一是将所给函数化为y＝Asin(ωx＋)(或y＝Acos(ωx＋))的形式再用T＝求解；二是利用图象的基本特征求解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高三数学教学与测试 题型：044

    求下列函数的最小正周期：

    (1)y＝tanx－cotx；

    (2)y＝sin(kx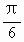－)sin(kx＋)，k≠0；

    (3)y＝．

    查看答案和解析>>

    科目：高中数学 来源：高三数学教学与测试 题型：044

    求下列函数的最小正周期：　　

    (1)y＝πx；

    (2)y＝cos(x)cos[(x－1)]；

    (3)y＝．

    查看答案和解析>>

    科目：高中数学 来源：中学教材全解　高中数学必修4　B版（配人民教育出版社实验教科书） 人教版　B版 题型：044

    求下列函数的最小正周期：

    (1)y＝－2sin(－x－1)；

    (2)y＝．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求下列函数的最小正周期.

    (1)y=3sin(2x+);

    (2)y=2cos(x-).

    查看答案和解析>>

    同步练习册答案