
| A. | $4\sqrt{3\sqrt{2}}$ | B. | $5\sqrt{4\sqrt{3\sqrt{2}}}$ | C. | $5\sqrt{4}$ | D. | $4\sqrt{3}$ |
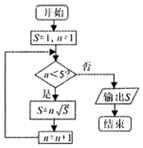
分析 模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时不满足条件n<5,退出循环,输出S的值4$\sqrt{3\sqrt{2}}$.
解答 解:模拟程序的运行,可得
S=1,n=1
满足条件n<5,执行循环体,S=1,n=2
满足条件n<5,执行循环体,S=2,n=3
满足条件n<5,执行循环体,S=3$\sqrt{2}$,n=4
满足条件n<5,执行循环体,S=4$\sqrt{3\sqrt{2}}$,n=5
不满足条件n<5,退出循环,输出S的值4$\sqrt{3\sqrt{2}}$.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,当循环次数有限或有规律时常采用模拟程序运行的方法来解决,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{16}{5}$ | C. | -2 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
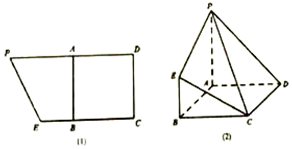 已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{4}{3}$,$\frac{1}{6}$] | B. | (0,$\frac{1}{6}$] | C. | (0,$\frac{1}{6}$) | D. | (-$\frac{4}{3}$,$\frac{1}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )
若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com