若
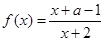
在区间
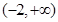
上是增函数,则实数
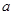
的取值范围是____________.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
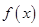
是定义在
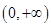
上的减函数,满足
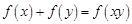
.
(1)求证:
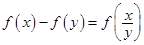
;
(2)若
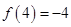
,解不等式
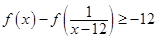
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
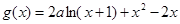
(1)当
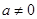
时,讨论函数
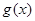
的单调性:
(2)若函数
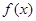
的图像上存在不同两点
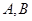
,设线段
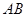
的中点为
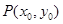
,使得
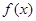
在点
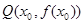
处的切线
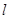
与直线
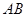
平行或重合,则说函数
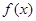
是“中值平衡函数”,切线
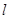
叫做函数
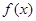
的“中值平衡切线”。试判断函数
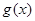
是否是“中值平衡函数”?若是,判断函数
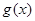
的“中值平衡切线”的条数;若不是,说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在R上的函数
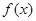
在(-∞,2)上是增函数,且
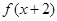
的图象关于
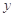
轴对称,则( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
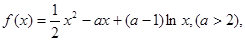
则
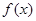
的单调增区间是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在
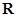
上的偶函数
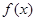
满足:对任意
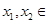
[0,+∞),且
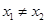
都有
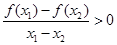
,则( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
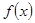
对于任意的
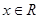
,导函数
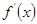
都存在,且满足
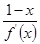
≤0,则必有( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
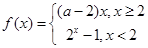
满足对任意实数
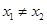
,都有
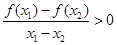
成立,则实数
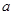
的取值范围为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
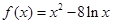
,
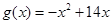
.
(Ⅰ) 求函数
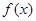
在点
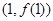
处的切线方程;
(Ⅱ) 若函数
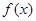
与
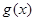
在区间
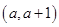
上均为增函数,求
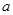
的取值范围;
(Ⅲ) 若方程
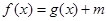
有唯一解,试求实数
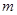
的值.
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案
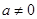 时,讨论函数
时,讨论函数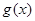 的单调性:
的单调性: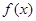 的图像上存在不同两点
的图像上存在不同两点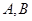 ,设线段
,设线段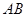 的中点为
的中点为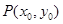 ,使得
,使得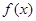 在点
在点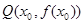 处的切线
处的切线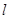 与直线
与直线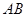 平行或重合,则说函数
平行或重合,则说函数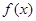 是“中值平衡函数”,切线
是“中值平衡函数”,切线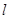 叫做函数
叫做函数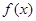 的“中值平衡切线”。试判断函数
的“中值平衡切线”。试判断函数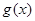 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数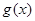 的“中值平衡切线”的条数;若不是,说明理由.
的“中值平衡切线”的条数;若不是,说明理由.