（09年湖南师大附中月考文）(12分)
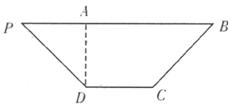
如图，在等腰梯形
中，
，
，
，
为
边上一点，且
，将
沿
折起，使平面
平面
．
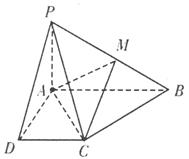
（1）求证：平面平面
；
（2）试在上找一点
，使截面
把几何体分成两部分，且
；
是否平行于平面． 科目：高中数学 来源： 题型：
（09年湖南师大附中月考文）(12分)
高三年级有7名同学分别获得校科技节某项比赛的一、二、三等奖，已知获一等奖的人数不少于1人，获二等奖的人数不少于2人，获三等奖的人数不少于3人．
(1)求恰有2人获一等奖的概率；
(2)求恰有3人获三等奖的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
（09年湖南师大附中月考理）(13分)
已知向量
，
，动点
到定直线
的距离等于
，并且满足
，其中
是坐标原点，
是参数。
（1）求动点的轨迹方程；
（2）当
时，若直线
与动点的轨迹相交于
、
两点，线段
的垂直平分线交
轴
，求
的取值范围；
的轨迹是一条圆锥曲线，其离心率
满足
，求的取值范围。查看答案和解析>>
科目：高中数学 来源： 题型：
（09年湖南师大附中月考理）（12分）
某种项目的射击比赛，开始时在距目标100m处射击，如果命中记3分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已经在150m处，这时命中记2分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已在200m处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分．已知射手甲在100m处击中目标的概率为
，他的命中率与目标的距离的平方成反比，且各次射击都是独立的．
(1)求这名射手分别在第二次、第三次射击中命中目标的概率及三次射击中命中目标的概率；
(2)设这名射手在比赛中得分数为
，求随机变量的概率分布列和数学期望．查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，又∵平面
平面
，∴
平面
平面
，∴平面
，………………………………………(6分)
、
，则
，∴
为
中点。……………………………………………………(8分)
，
平面
平面
平面
平面
，∴平面
平面
与平面
矛盾 
与平面
，其中
。
(1)当
时，求
值的集合；
|的最大值。
，数列
满足：
，
；
是等差数列；