
【题目】将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在
个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在 ![]() 的最大值为( )
的最大值为( )
A.0
B.![]()
C.![]()
D.1
【答案】D
【解析】解:将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位长度后, 可得函数g(x)=sin(2x+
个单位长度后, 可得函数g(x)=sin(2x+ ![]() +φ)的图象,根据所得图象关于原点对称,
+φ)的图象,根据所得图象关于原点对称,
可得 ![]() +φ=π,∴φ=
+φ=π,∴φ= ![]() ,f(x)=sin(2x+
,f(x)=sin(2x+ ![]() ).
).
在 ![]() 上,2x+
上,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],故当2x+
],故当2x+ ![]() =
= ![]() 时,f(x)=sin(2x+
时,f(x)=sin(2x+ ![]() )取得最大值为1,
)取得最大值为1,
故选:D.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了
元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了![]() 个面包,以
个面包,以![]() (单位:个,
(单位:个,![]() )表示面包的需求量,
)表示面包的需求量,![]() (单位:元)表示利润.
(单位:元)表示利润.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各个城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调研机构在该市随机抽取了
市的使用情况,某调研机构在该市随机抽取了![]() 位市民进行调查,得到的
位市民进行调查,得到的![]() 列联表(单位:人)
列联表(单位:人)

(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为使用共享单车的情况与年龄有关?(结果保留3位小数)
的前提下认为使用共享单车的情况与年龄有关?(结果保留3位小数)
(2)现从所抽取的![]() 岁以上的市民中利用分层抽样的方法再抽取5人
岁以上的市民中利用分层抽样的方法再抽取5人
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机抽取2人赠送一件礼物,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式及数据:![]() ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]()
(1)求椭圆![]() 的标准方程
的标准方程
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆与不同的两点
交椭圆与不同的两点![]() ,且满足
,且满足![]() (其中
(其中![]() 为坐标原点)。若存在,求出直线
为坐标原点)。若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线C: ![]() =1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=
=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ= ![]() ,且
,且 ![]() |,则双曲线C的离心率为( )
|,则双曲线C的离心率为( ) 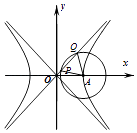
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有高一、高二、高三三个年级,已知高一、高二、高三的学生数之比为2:3;5,现从该学校中抽取一个容量为100的样本,从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为 ![]() ,则该学校学生的总数为( )
,则该学校学生的总数为( )
A.200
B.400
C.500
D.1000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)经过点(
=1(a>b>0)经过点( ![]() ,1),以原点为圆心,椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心,椭圆短半轴长为半径的圆经过椭圆的焦点.
(1)求椭圆C的方程;
(2)设过点(﹣1,0)的直线l与椭圆C相交于A、B两点,试问在x轴上是否存在一个定点M,使得 ![]()
![]() 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com