练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】综合题。
    （1）已知x＜ ，求函数y=4x﹣2+ 的最大值；
    （2）已知x＞0，y＞0且 =1，求x+y的最小值．

    【答案】
    （1）解：∵x＜ ，∴4x﹣5＜0．

    ∴y=4x﹣5+ +3=﹣[（5﹣4x）+ ]+3

    ≤﹣2 +3=1，当且仅当x=1时取等号．

    ∴ymax=1


    （2）解：∵x＞0，y＞0且 =1，

    ∴x+y=（x+y） =10+ ≥10+2 =16，当且仅当y=3x=12时取等号．

    ∴x+y的最小值为16


    【解析】（1）变形利用基本不等式的性质即可得出；（2）利用“乘1法”和基本不等式的性质即可得出．
    【考点精析】利用基本不等式对题目进行判断即可得到答案，需要熟知基本不等式：,（当且仅当时取到等号）；变形公式：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三视图，第一次切削，将该毛坯得到一个表面积最大的长方体，第二次切削沿长方体的对角面刨开，得到两个三棱柱，第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马，则阳马与鳖臑的体积之比为（ ）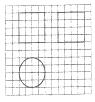
    A.3：1
    B.2：1
    C.1：1
    D.1：2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥P﹣ABCD中，底面ABCD为直角梯形，AB⊥AD，BC∥AD，且AB=BC=2，AD=3，PA⊥平面ABCD且PA=2，则PB与平面PCD所成角的正弦值为（ ）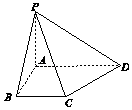
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥P﹣ABCD中，PB⊥底面ABCD，CD⊥PD．底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3．点E在棱PA上，且PE=2EA． （Ⅰ）求异面直线PA与CD所成的角；
    （Ⅱ）求证：PC∥平面EBD；
    （Ⅲ）求二面角A﹣BE﹣D的大小．（用反三角函数表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列不等式的解集是空集的是（ ）
    A.x2﹣x+1＞0
    B.﹣2x2+x+1＞0
    C.2x﹣x2＞5
    D.x2+x＞2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定点F1（0，﹣3）、F2（0，3），动点P满足条件|PF1|+|PF2|=a+ （a＞0），则点P的轨迹是（ ）
    A.椭圆
    B.线段
    C.不存在
    D.椭圆或线段

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD中PA⊥平面ABCD，且PA=4PQ=4，底面为直角梯形， ∠CDA=∠BAD=90°， ，M，N分别是PD，PB的中点．

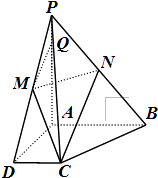
    （1）求证：MQ∥平面PCB；
    （2）求截面MCN与底面ABCD所成二面角的大小；
    （3）求点A到平面MCN的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x>0,y>0,且2x+8y-xy=0,求:
    （1）xy的最小值;
    （2）x+ y的最小值.

    查看答案和解析>>

    同步练习册答案