
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
分析 设等腰直角三角形OAB的顶点A(x1,y1),B(x2,y2),利用OA=OB可求得x1=x2,进而可求得AB=4p,从而可得S△OAB.设过点N的直线方程为y=k(x+1),代入y2=4x,过M作准线的垂线,垂足为A,则|MF|=|MA|,考虑直线与抛物线相切及倾斜角为0°,即可得出p.设M 到准线的距离等于d,由抛物线的定义,化简为 $\frac{|OM|}{|MF|}$=$\frac{|MO|}{d}$=$\sqrt{\frac{{m}^{2}+4m}{(m+1)^{2}}}$,换元,利用基本不等式求得最大值.
解答 解:设等腰直角三角形OAB的顶点A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2.
由OA=OB得:x12+y12=x22+y22,
∴x12-x22+2px1-2px2=0,即(x1-x2)(x1+x2+2p)=0,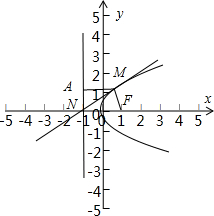
∵x1>0,x2>0,2p>0,
∴x1=x2,即A,B关于x轴对称.
∴直线OA的方程为:y=xtan45°=x,
与抛物线联立,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2p}\\{y=2p}\end{array}\right.$,
故AB=4p,
∴S△OAB=$\frac{1}{2}$×2p×4p=4p2.
∵△AOB的面积为16,∴p=2;
焦点F(1,0),设M(m,n),则n2=4m,m>0,设M 到准线x=-1的距离等于d,
则$\frac{|OM|}{|MF|}$=$\frac{|MO|}{d}$=$\sqrt{\frac{{m}^{2}+4m}{(m+1)^{2}}}$.
令 m+1=t,t>1,则$\frac{|OM|}{|MF|}$=$\sqrt{-3(\frac{1}{t}-\frac{1}{3})^{2}+\frac{4}{3}}$≤$\frac{2\sqrt{3}}{3}$(当且仅当 t=3时,等号成立).
故 $\frac{|OM|}{|MF|}$的最大值为$\frac{2\sqrt{3}}{3}$,
故选C.
点评 本题考查抛物线的简单性质,求得A,B关于x轴对称是关键,考查抛物线的定义,基本不等式的应用,体现了换元的思想,正确运用抛物线的定义是关键,属于难题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {(1,1)} | C. | {(x,y)|x+y-2=0} | D. | {(x,y)|3x-2y-1=0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
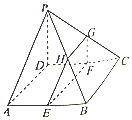 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
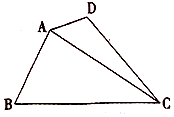 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com