
【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为![]() ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为![]() ,现从
,现从![]() ,
,![]() 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到点
到点![]() 的距离比它到
的距离比它到![]() 轴的距离多1,记点
轴的距离多1,记点![]() 的轨迹为
的轨迹为![]() ;
;
(1)求轨迹![]() 的方程;
的方程;
(2)求定点![]() 到轨迹
到轨迹![]() 上任意一点
上任意一点![]() 的距离
的距离![]() 的最小值;
的最小值;
(3)设斜率为![]() 的直线
的直线![]() 过定点
过定点![]() ,求直线
,求直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时![]() 的相应取值范围.
的相应取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )
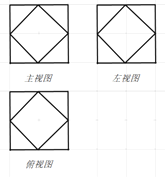
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于统计数据的分析,有以下几个结论,其中正确的个数为( )
①利用残差进行回归分析时,若残差点比较均匀地落在宽度较窄的水平带状区域内,则说明线性回归模型的拟合精度较高;
②将一组数据中的每个数据都减去同一个数后,期望与方差均没有变化;
③调查剧院中观众观后感时,从50排(每排人数相同)中任意抽取一排的人进行调查是分层抽样法;
④已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-![]() 中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB
中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB![]() ,∠BA
,∠BA![]() =60°,AB=A
=60°,AB=A![]() =2BC=2CD=2
=2BC=2CD=2
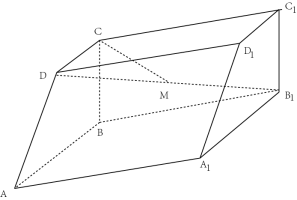
(1)求证:BC⊥A![]() ;
;
(2)求二面角D-A![]() -B的余弦值;
-B的余弦值;
(3)在线段D![]() 上是否存在点M,使得CM∥平面DA
上是否存在点M,使得CM∥平面DA![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com