
【题目】设数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)在![]() 中,将
中,将![]() 代
代![]() 得:
得: ![]() ,由两式作商得:
,由两式作商得:![]() ,问题得解。
,问题得解。
(2)利用(1)中结果求得![]() ,分组求和,再利用等差数列前
,分组求和,再利用等差数列前![]() 项和公式及乘公比错位相减法分别求和即可得解。
项和公式及乘公比错位相减法分别求和即可得解。
(1)由n=1得![]() ,
,
因为![]() ,
,
当n≥2时,![]() ,
,
由两式作商得:![]() (n>1且n∈N*),
(n>1且n∈N*),
又因为![]() 符合上式,
符合上式,
所以![]() (n∈N*).
(n∈N*).
(2)设![]() ,
,
则bn=n+n·2n,
所以Sn=b1+b2+…+bn=(1+2+…+n)+![]()
设Tn=2+2·22+3·23+…+(n-1)·2n-1+n·2n,①
所以2Tn=22+2·23+…(n-2)·2n-1+(n-1)·2n+n·2n+1,②
①-②得:-Tn=2+22+23+…+2n-n·2n+1,
所以Tn=(n-1)·2n+1+2.
所以![]() ,
,
即![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在以P为顶点的圆锥中,母线长为![]() ,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切.连接BC交圆于点D,连接PD,PC,E是PC的中点,连接OE,ED.
,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切.连接BC交圆于点D,连接PD,PC,E是PC的中点,连接OE,ED.
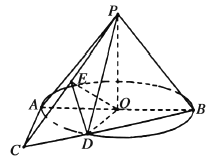
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若二面角![]() 的大小为
的大小为![]() ,求面PAC与面DOE所成锐二面角的余弦值.
,求面PAC与面DOE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,过
的焦点,过![]() 的动直线交抛物线
的动直线交抛物线![]() 于
于![]() ,
,![]() 两点.当直线与
两点.当直线与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 的斜率为1且与抛物线的准线
的斜率为1且与抛物线的准线![]() 相交于点
相交于点![]() ,抛物线
,抛物线![]() 上存在点
上存在点![]() 使得直线
使得直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,求点
的斜率成等差数列,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,网上购物已经成为人们消费的一种习惯.假设某淘宝店的一种装饰品每月的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)之间满足如下的关系式:
(单位:元/件)之间满足如下的关系式:![]() 为常数.已知销售价格为
为常数.已知销售价格为![]() 元/件时,每月可售出
元/件时,每月可售出![]() 千件.
千件.
(1)求实数![]() 的值;
的值;
(2)假设该淘宝店员工工资、办公等所有的成本折合为每件2元(只考虑销售出的装饰品件数),试确定销售价格![]() 的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四![]() 年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量
年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() (单位:万只)与相应年份
(单位:万只)与相应年份![]() (序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
年份序号 |
|
|
|
|
|
|
|
|
|
年养殖山羊 |
|
|
|
|
|
|
|
|
|
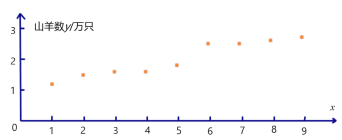
(1)根据表中的数据和所给统计量,求![]() 关于
关于![]() 的线性回归方程(参考统计量:
的线性回归方程(参考统计量:![]() ,
,![]() ;
;
(2)李四提供了该县山羊养殖场的个数![]() (单位:个)关于
(单位:个)关于![]() 的回归方程
的回归方程![]() .
.
试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]()
![]()
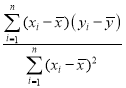 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
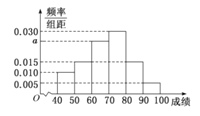
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中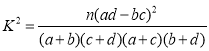 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com