
分析 (1)求导,由导数的几何意义,求得tanα=2,由诱导公式即可求得答案;
(2)由正弦定理代入$acosC+\frac{1}{2}c=b$,整理求得A,由正弦定理得:表示出△ABC的周长l,利用正弦函数的图象及性质即可求得△ABC的周长l的取值范围.
解答 解:(1)∵f′(x)=2+2cosx-sinx,f′(α)=2,
即tanα=2,
∴$\frac{sin(π-α)+cos(-α)}{{2cos(\frac{π}{2}-α)+cos(2π-α)}}=\frac{sinα+cosα}{2sinα+cosα}=\frac{tanα+1}{2tanα+1}=\frac{3}{5}$,
∴$\frac{sin(π-α)+cos(-α)}{{2cos(\frac{π}{2}-α)+cos(2π-α)}}$的值$\frac{3}{5}$;…(5分)
(2)由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,
则a=2RsinA,b=2RsinB,c=2RsinC,
由$acosC+\frac{1}{2}c=b$,则sinAcosC+$\frac{1}{2}$sinC=sinB,
∴$sinAcosC+\frac{1}{2}sinC=sin(A+C)=sinAcosC+cosAsinC$,
∴$\frac{1}{2}sinC=cosAsinC$,
∵C∈(0,π),∴sinC≠0,
∴$cosA=\frac{1}{2}$,又0<A<π,
∴$A=\frac{π}{3}$…(8分)
由正弦定理得:$b=\frac{asinB}{sinA}=\frac{2}{{\sqrt{3}}}sinB$,
$c=\frac{2}{{\sqrt{3}}}sinC$∴$l=a+b+c=1+\frac{2}{{\sqrt{3}}}(sinB+sinC)$,
=$1+\frac{2}{{\sqrt{3}}}[sinB+sin(A+B)]$,
=$1+2(\frac{{\sqrt{3}}}{2}sinB$$+\frac{1}{2}cosB)$,
=$1+2sin(B+\frac{π}{6})$…(10分)
∵$A=\frac{π}{3}$,
∴$B∈(0,\frac{2π}{3})$,
∴$B+\frac{π}{6}∈(\frac{π}{6},\frac{5π}{6})$,
∴$sin(B+\frac{π}{6})∈(\frac{1}{2},1]$ …(11分)
∴△ABC的周长l的取值范围(2,3]…(12分)
点评 本题考查诱导公式,正弦定理,正弦函数的性质,考查计算能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 当α=0时,幂函数的图象是一条直线 | |
| B. | 幂函数的图象都经过(0,0)和(1,1)两个点 | |
| C. | 若函数f(x)为奇函数,则f(x)在定义域内是增函数 | |
| D. | 幂函数f(x)的图象不可能在第四象限内 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 羊毛颜色 | 每匹需要/kg | 供应量/kg | |
| 布料A | 布料B | ||
| 红 | 3 | 3 | 1050 |
| 绿 | 4 | 2 | 1200 |
| 黄 | 2 | 6 | 1800 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
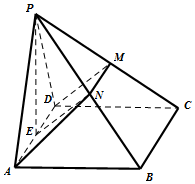 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
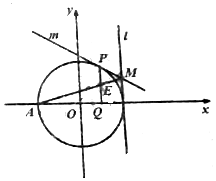 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com