
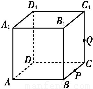
如图,正方体ABCD A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
①当0<CQ<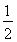 时,S为四边形;
时,S为四边形;
②当CQ=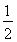 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=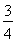 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=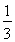 ;
;
④当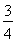 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为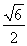 .
.
①②③⑤
【解析】利用平面的基本性质结合特殊四边形的判定与性质求解.
①当0<CQ<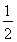 时,如图(1).
时,如图(1).
在平面AA1D1D内,作AE∥PQ,
显然E在棱DD1上,连接EQ,
则S是四边形APQE.
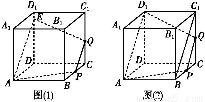
②当CQ=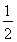 时,如图(2).
时,如图(2).
显然PQ∥BC1∥AD1,连接D1Q,
则S是等腰梯形.
③当CQ=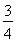 时,如图(3).
时,如图(3).
作BF∥PQ交CC1的延长线于点F,则C1F=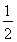 .
.
作AE∥BF,交DD1的延长线于点E,D1E=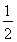 ,AE∥PQ,
,AE∥PQ,
连接EQ交C1D1于点R,由于Rt△RC1Q∽Rt△RD1E,
∴C1Q∶D1E=C1R∶RD1=1∶2,
∴C1R=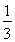 .
.
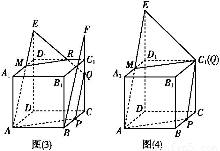
④当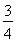 <CQ<1时,如图(3),连接RM(点M为AE与A1D1交点),显然S为五边形APQRM.
<CQ<1时,如图(3),连接RM(点M为AE与A1D1交点),显然S为五边形APQRM.
⑤当CQ=1时,如图(4).
同③可作AE∥PQ交DD1的延长线于点E,交A1D1于点M,显然点M为A1D1的中点,所以S为菱形APQM,其面积为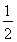 MP×AQ=
MP×AQ=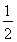 ×
×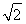 ×
×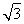 =
=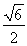 .
.


科目:高中数学 来源: 题型:
 如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长.
如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长.查看答案和解析>>
科目:高中数学 来源: 题型:
 (文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:
(文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:查看答案和解析>>
科目:高中数学 来源: 题型:
 甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=
甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=| 2 |
| AE |
| D1B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com