
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )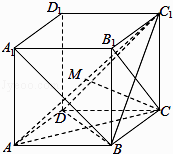
A.0个
B.1个
C.2个
D.3个
【答案】D
【解析】解:①在△A1BD中,每条边都是 ![]() ,即为等边三角形,∴A1B与A1D所成角为60°, 又B1C∥A1D,∴直线A1B与B1C所成的角为60°,正确;
,即为等边三角形,∴A1B与A1D所成角为60°, 又B1C∥A1D,∴直线A1B与B1C所成的角为60°,正确;
②如图,由正方体可得平面BDC1⊥平面ACC1 , 当M点位于AC1上,且使CM⊥平面BDC1时,直线CM与平面BDC1所成角的正弦值最大为1,
当M与C1重合时,连接CM交平面BDC1所得斜线最长,直线CM与平面BDC1所成角的正弦值最小等于 ![]() ,
,
∴直线CM与平面BDC1所成角的正弦值的取值范围是[ ![]() ,1],正确;
,1],正确;
③连接B1P,B1Q,设D1到平面B1AC的距离为h,则h= ![]() ,B1到直线AC的距离为
,B1到直线AC的距离为 ![]() ,
,
则四面体PQB1D1的体积V= ![]() ,正确.
,正确.
∴正确的命题是①②③.
故选:D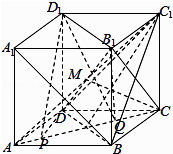
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx+2 ![]() cosωxsinωx+sin(ωx+
cosωxsinωx+sin(ωx+ ![]() )sin(ωx﹣
)sin(ωx﹣ ![]() )(ω>0),且f(x)的最小正周期为π.
)(ω>0),且f(x)的最小正周期为π.
(1)求ω的值;
(2)求函数f(x)在区间(0,π)上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ1),g(x)=cos(4x+φ2),|φ1|≤ ![]() ,|φ2|≤
,|φ2|≤ ![]() . 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x=
. 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x= ![]() kπ+φ(k∈Z)是函数g(x)的对称轴;
kπ+φ(k∈Z)是函数g(x)的对称轴;
命题②:若点P(φ,0)是函数f(x)和g(x)的对称中心,则点Q( ![]() +φ,0)(k∈Z)是函数f(x)的中心对称.( )
+φ,0)(k∈Z)是函数f(x)的中心对称.( )
A.命题①②都正确
B.命题①②都不正确
C.命题①正确,命题②不正确
D.命题①不正确,命题②正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+cosα﹣2﹣x+cosα , x∈R,且 ![]() .
.
(1)若0≤α≤π,求α的值;
(2)当m<1时,证明:f(m|cosθ|)+f(1﹣m)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数集R,集合A={x|1<x<3},集合B={x|y= ![]() },则A∩(RB)=( )
},则A∩(RB)=( )
A.{x|1<x≤2}
B.{x|1<x<3}
C.{x|2≤x<3}
D.{x|1<x<2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 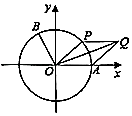
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() ),
), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣
﹣ ![]() )2+2S2﹣
)2+2S2﹣ ![]() ,求f(θ)的最值及此时θ的值.
,求f(θ)的最值及此时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com