
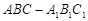 中,△
中,△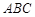 为等腰直角三角形,∠
为等腰直角三角形,∠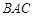 =
=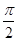 ,且
,且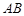 =
=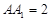 ,
,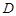 、
、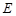 、
、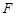 分别为
分别为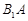 、
、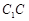 、
、 的中点.
的中点.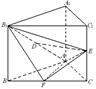
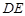 ∥平面
∥平面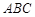 ;
;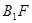 ⊥平面
⊥平面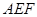 ;
;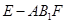 的体积.
的体积.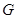 是
是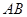 的中点,连结
的中点,连结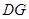 ,则
,则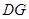 平行且等于
平行且等于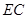 ,所以四边形
,所以四边形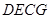 是平行四边形,所以
是平行四边形,所以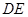 //
//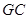 ,从而
,从而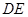 ∥平面
∥平面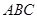 .
.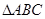 为等腰直角三角形,
为等腰直角三角形,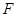 为
为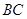 的中点,∴
的中点,∴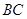 ⊥
⊥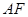 ,又∵
,又∵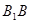 ⊥平面
⊥平面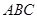 ,可证
,可证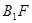 ⊥
⊥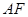 ∵
∵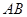 =
=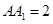 ,∴
,∴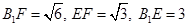 ,∴
,∴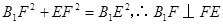 ,∵
,∵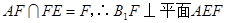
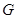 是
是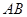 的中点,连结
的中点,连结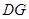 ,则
,则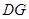 平行且等于
平行且等于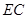 ,…(2分)
,…(2分)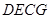 是平行四边形,所以
是平行四边形,所以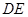 //
//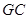 ,
,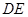 ∥平面
∥平面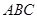 . …………(4分)
. …………(4分)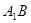 、
、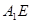 ,并延长
,并延长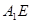 交
交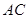 的延长线于点
的延长线于点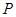 ,连接
,连接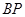 .
.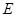 为
为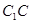 的中点,
的中点,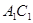 ‖
‖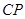 ,可证
,可证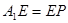 ……(2分)
……(2分)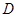 、
、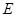 是
是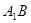 、
、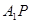 的中点,∴
的中点,∴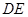 ‖
‖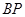 ,又∵
,又∵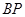
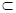 平面
平面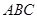 ,
,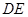
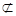 平面
平面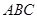 ,∴
,∴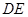 ∥平面
∥平面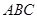 ………(4分)
………(4分)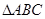 为等腰直角三角形,
为等腰直角三角形, 为
为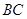 的中点,∴
的中点,∴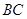 ⊥
⊥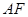 ,
,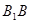 ⊥平面
⊥平面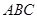 ,可证
,可证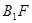 ⊥
⊥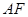 ……(6分)
……(6分)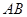 =
=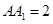 ,∴
,∴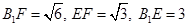 ,
,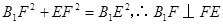 ,
,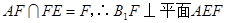 ……(8分)
……(8分)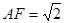 ,
,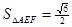 ,…………(10分)
,…………(10分)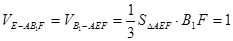 …………(12分)
…………(12分)

 考前必练系列答案
考前必练系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
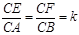 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 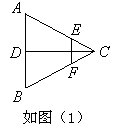
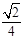 ,求k的值.
,求k的值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
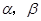 截球O的两个截面圆的半径分别为1和
截球O的两个截面圆的半径分别为1和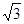 .若二面角
.若二面角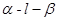 的平面角为150°,则球O的表面积为
的平面角为150°,则球O的表面积为A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
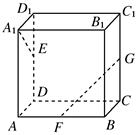
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com