
【题目】已知函数![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的单调递减区间;
的单调递减区间;
(3)当![]() 时,若对任意的
时,若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据偶函数的定义,结合题意,得到![]() ,进而可求出结果;
,进而可求出结果;
(2)先由题意得到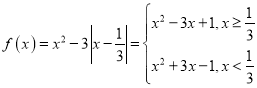 ,根据二次函数的性质,即可得出单调减区间;
,根据二次函数的性质,即可得出单调减区间;
(3)先由题意得到![]() 在
在![]() 上恒成立,令
上恒成立,令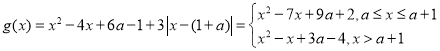 ,根据二次函数单调性,得出函数的最小值,只需
,根据二次函数单调性,得出函数的最小值,只需![]() 即可求出结果.
即可求出结果.
(1)因为函数![]() 为偶函数,
为偶函数,
所以![]() ,即
,即![]() ,即
,即![]() ,因此
,因此![]() ;
;
(2)因为![]() ,所以
,所以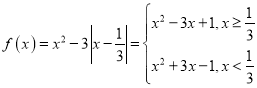 ,
,
因为函数![]() 的对称轴为
的对称轴为![]() ,开口向上;
,开口向上;
所以当![]() 时,函数
时,函数![]() 单调递减;当
单调递减;当![]() 时,函数
时,函数![]() 单调递增;
单调递增;
又函数![]() 的对称轴为
的对称轴为![]() ,开口向上;
,开口向上;
所以当![]() 时,函数
时,函数![]() 单调递增;当
单调递增;当![]() 时,函数
时,函数![]() 单调递减;
单调递减;
因此,函数![]() 的单调递减区间为:
的单调递减区间为:![]() 和
和![]() ;
;
(3)由题意,不等式![]() 可化为
可化为![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则只需
,则只需![]() 即可;
即可;
因为![]() ,所以
,所以![]() ,
,
因此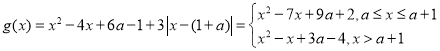 ,
,
当![]() 时,函数
时,函数![]() 开口向上,对称轴为:
开口向上,对称轴为:![]() ,
,
所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 开口向上,对称轴为
开口向上,对称轴为![]() ;
;
所以函数![]() 在
在![]() 上单调递增;
上单调递增;
因此![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() .
.
即实数![]() 的取值范围为
的取值范围为![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,求满足如下条件的最小四位整数![]() :第2017行的第
:第2017行的第![]() 项为2的正整数幂.已知
项为2的正整数幂.已知![]() ,那么该款软件的激活码是( )
,那么该款软件的激活码是( )

A. 1040 B. 1045 C. 1060 D. 1065
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com