
【题目】如图,已知直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.

【答案】(Ⅰ)1;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)可以设直线![]() 的方程为
的方程为![]() ,再设直线
,再设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,于是分别表示出
,于是分别表示出![]() ,由直线对称性可知,
,由直线对称性可知, ![]() 所在直线与
所在直线与![]() 垂直,且
垂直,且![]() 中点在
中点在![]() 上,于是整理得出
上,于是整理得出![]() 的值;(Ⅱ)本问考查椭圆中直线过定点问题,设
的值;(Ⅱ)本问考查椭圆中直线过定点问题,设![]() ,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
试题解析:(Ⅰ)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]()

直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,∴
,∴![]()
![]() ,由
,由![]()
得![]() ……..①
……..①
由![]() 得
得![]() …….②,
…….②,
由①②得 ![]()
![]() .
.
(Ⅱ)设点![]() ,由
,由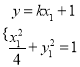 得
得![]() ,
,
∴![]() ,∴
,∴![]() .
.
同理: ![]() ,
, ![]()

![]() ,∴
,∴![]()
即: 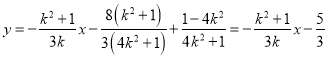
∴当![]() 变化时,直线
变化时,直线![]() 过定点
过定点![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点为
的左,右焦点为![]() ,左,右顶点为
,左,右顶点为![]() ,过点
,过点![]() 的
的
直线![]() 分别交椭圆于点
分别交椭圆于点![]() .
.
(1)设动点![]() ,满足
,满足![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(2)当![]() 时,求
时,求![]() 点的坐标;
点的坐标;
(3)设![]() ,求证:直线
,求证:直线![]() 过
过![]() 轴上的定点.
轴上的定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|

(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
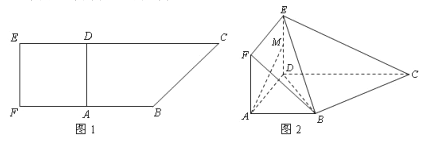
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1 , y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD//BC,且BC⊥PB,△PAB是等边三角形,DA=AB=2,BC=![]() AD,E是线段AB的中点.
AD,E是线段AB的中点.
(I)求证:PE⊥CD;
(II)求PC与平面PDE所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过 变换后得曲线
变换后得曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() 且
且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com