
分析 (1)根据导数的几何意义,即可求出;
(2)根据导数和函数的极值的关系即可求出,先求导,再判断单调性,继而得到极值.
解答 解:(1)f'(x)=x2-(a-1)x+b,f(x)在点P(-1,f(-1))处的切线与y轴垂直,
则f'(-1)=1+(a-1)+b=a+b=0,即a与b的关系式为a+b=0;
(2)由(1)可知b=-a,则f(x)=$\frac{1}{3}{x^3}-\frac{1}{2}(a-1){x^2}$-ax+1,
∴f'(x)=x2-(a-1)x-a=(x-a)(x+1),其中a>0
令f'(x)>0得,x<-1或x>a;令f'(x)<0得,-1<x<a,
∴f(x)在(-∞,-1)上单调递增,在(-1,a)上单调递减,在(a,+∞)上单调递增
∴f(x)极大值=f(-1)=$-\frac{1}{3}$-$\frac{1}{2}$(a-1)+a+1=$\frac{1}{2}$a+$\frac{7}{6}$,
f(x)极小值=f(a)=$\frac{1}{3}$a3-$\frac{1}{2}$a2(a-1)-a2+1=-$\frac{1}{6}$a3-$\frac{1}{2}$a2+1,
∴f(x)有极大值为$\frac{1}{2}$a+$\frac{7}{6}$,极小值为-$\frac{1}{6}$a3-$\frac{1}{2}$a2+1.
点评 本题重点考查利用导数研究函数的性质,解题时要认真审题,注意导数性质的合理运用,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
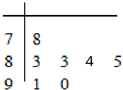 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85和6.8 | B. | 85和1.6 | C. | 86和6.8 | D. | 86和1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 有红、黄、蓝、白4种颜色的小球,每种小球数量不限且它们除颜色不同外,其余完全相同,将小球放入如图所示编号为1,2,3,4,5的盒子中,每个盒子只放一只小球.
有红、黄、蓝、白4种颜色的小球,每种小球数量不限且它们除颜色不同外,其余完全相同,将小球放入如图所示编号为1,2,3,4,5的盒子中,每个盒子只放一只小球.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞)上单调递减 | B. | $(\frac{1}{e},+∞)$上单调递减 | C. | $(0,\frac{1}{e})$上单调递减 | D. | (0,+∞)上单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com