解:(1)由已知得t=0,f′(x)=2mx+n,
则f′(0)=n=0,f′(-1)=-2m+n=-2,从而n=0,m=1,
∴f(x)=x
2f′(x)=2x,g′(x)=3ax
2+b.
由f(1)=g(1),f′(1)=g′(1),得a+b-3=1,3a+b=2,解得a=-1,b=5.∴g(x)=-x
3+5x-3(x>0).
(2)F(x)=f(x)-g(x)=x
3+x
2-5x+3(x>0),
求导数得F′(x)=3x
2+2x-5=(x-1)(3x+5).∴F(x)在(0,1)单调递减,在(1,+∞)单调递增,从而F(x)的极小值为F(1)=0.
(3)因f(x)与g(x)有一个公共点(1,1),而函数f(x)在点(1,1)的切线方程为y=2x-1.
下面验证
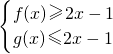
都成立即可.
由x
2-2x+1≥0,得x
2≥2x-1,知f(x)≥2x-1恒成立.
设h(x)=-x
3+5x-3-(2x-1),即h(x)=-x
3+3x-2(x>0),
求导数得h′(x)=-3x
2+3=-3(x-1)(x+1)(x>0),∴h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以h(x)=-x
3+5x-3-(2x-1)的最大值为h(1)=0,
所以-x
3+5x-3≤2x-1恒成立.
故存在这样的实常数k和m,且k=2,m=-1.
分析:(1)由已知得t=0,求出导数f′(x)=2mx+n,由f′(0)=n=0,f′(-1)=-2m+n=-2,解得n=0,m=1,得出f(x)=x
2f′(x)=2x,g′(x)=3ax
2+b.再由条件列出关于a,b的方程,求得a,b即可写出函数f(x),g(x)的解析式;
(2)F(x)=f(x)-g(x)=x
3+x
2-5x+3(x>0),先确定函数的定义域然后求出函数的导涵数Fˊ(x),在函数的定义域内解不等式Fˊ(x)>0和Fˊ(x)<0,即可求出函数的单调区间,然后根据极值的定义进行判定极值即可.(3)对于存在性问题,可先假设存在,即假设存在函数f(x)在点(1,1)的切线方程为y=2x-1满足条件,再利用导数,求出h(x)=-x
3+5x-3-(2x-1)的最大值进行验证,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本小题主要考查函数的导数,单调性,利用导数求闭区间上函数的最值等基础知识,考查综合利用数学知识分析问题、解决问题的能力,注意(3)的处理存在性问题的一般方法,首先假设存在,进而根据题意、结合有关性质,化简、转化、计算,最后得到结论.

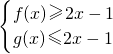 都成立即可.
都成立即可.
