
����Ŀ��ij���������� ![]() ��
�� ![]() ����ʼ���У�ͨ���г����飬�õ���������ֲ�ɱ�
����ʼ���У�ͨ���г����飬�õ���������ֲ�ɱ� ![]() (����ÿ
(����ÿ ![]() ��������������ֲ�ɱ�����λ��Ԫ)������ʱ��
��������������ֲ�ɱ�����λ��Ԫ)������ʱ�� ![]() (��λ����)���������±���
(��λ����)���������±���
����ʱ�� | 50 | 110 | 250 |
��ֲ�ɱ� | 150 | 108 | 150 |
��1�������ϱ����ݣ������к�����ѡȡһ������������������ֲ�ɱ�������ʱ�� ![]() �ı仯��ϵ��
�ı仯��ϵ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���������������ʽ��
���������������ʽ��
��2��������ѡȡ�ĺ���������������ֲ�ɱ����ʱ�����������������ֲ�ɱ���
���𰸡�
��1���⣺���ṩ������֪����������������ֲ�ɱ� ![]() ������ʱ��
������ʱ�� ![]() �ı仯��ϵ�ĺ����������dz����������Ӷ��ú���
�ı仯��ϵ�ĺ����������dz����������Ӷ��ú��� ![]() ��
�� ![]() ��
�� ![]() �е�����һ����������ʱ��Ӧ��
�е�����һ����������ʱ��Ӧ�� ![]() ������ʱ��������������Ϊ��������������������ṩ�����ݲ��Ǻϣ����ԣ�ѡȡ���κ���
������ʱ��������������Ϊ��������������������ṩ�����ݲ��Ǻϣ����ԣ�ѡȡ���κ��� ![]() ����������
����������
���������ṩ���������ݷֱ���� ![]() ���õ�
���õ�
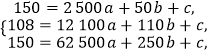 �ⷽ�����
�ⷽ����� 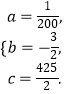
����������������ֲ�ɱ� ![]() ������ʱ��
������ʱ�� ![]() �ı仯��ϵ�ĺ���Ϊ��
�ı仯��ϵ�ĺ���Ϊ�� ![]()
��2���⣺�� 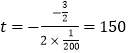 ʱ����������ֲ�ɱ����Ϊ��
ʱ����������ֲ�ɱ����Ϊ�� ![]() (Ԫ)
(Ԫ)
��������(1)������������֪�г������Ľ���ʽ���ɡ�(2)���ͬ�������ֵ���������ɡ�


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ��ͼ��ΪC�������½�������ȷ������д��������ȷ���۵ı�ţ���
��ͼ��ΪC�������½�������ȷ������д��������ȷ���۵ı�ţ���
��ͼ��C����ֱ�� ![]() �Գƣ�
�Գƣ�
��ͼ��C���ڵ� ![]() �Գƣ�
�Գƣ�
�ۺ���f��x�������� ![]() ���Ǽ�������
���Ǽ�������
�ܰѺ��� ![]() ��ͼ���ϵ�ĺ�����ѹ��Ϊԭ����һ�루�����겻�䣩���Եõ�ͼ��C��
��ͼ���ϵ�ĺ�����ѹ��Ϊԭ����һ�루�����겻�䣩���Եõ�ͼ��C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�����ߵ��е�ΪS��M��N��T�������ĸ��е��С������SMNT����������ABCD��������SMNT�ƶԽ���AC��תһ�ܵõ���������ת���������μ�ΪV1 �� V2 �� ��V1��V2=�� �� 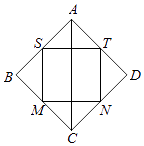
A.8��1
B.2��1
C.4��3
D.8��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() x��lnx��x��0��������f��x���� ��
x��lnx��x��0��������f��x���� ��
A.�����䣨0��1��������㣬�����䣨1��+�ޣ��������
B.�����䣨0��1��������㣬�����䣨1��+�ޣ��������
C.�����䣨0��3������3��+�ޣ��������
D.�����䣨0��3������3��+�ޣ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ij�ֲ�Ʒÿ����Ҫ�̶�Ͷ�� ![]() ��Ԫ������ÿ����
��Ԫ������ÿ���� ![]() ���ò�Ʒ����Ҫ����Ͷ��
���ò�Ʒ����Ҫ����Ͷ�� ![]() ��Ԫ�������Ϊ
��Ԫ�������Ϊ ![]() ������
������ ![]() ʱ��������������Ϊ
ʱ��������������Ϊ ![]() ��Ԫ����
��Ԫ���� ![]() ʱ��������������Ϊ
ʱ��������������Ϊ ![]() ��Ԫ���Ǹù����������������ֲ�Ʒ���õ�������Ϊ
��Ԫ���Ǹù����������������ֲ�Ʒ���õ�������Ϊ ![]() ��Ԫ��
��Ԫ��
��1���� ![]() ����Ԫ������
����Ԫ������ ![]() �������ĺ�����ϵʽ��
�������ĺ�����ϵʽ��
��2���ù����������Ϊ���ټ�ʱ���������������������ֵ��������������������������Ͷ�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���б߷ֱ�Ϊa��b��c���� ![]() �� �������A��
�� �������A��
������ ![]() �����ж�bcȡ�����ֵʱ��ABC��״��
�����ж�bcȡ�����ֵʱ��ABC��״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵õ����� ![]() ��ͼ���Խ�����y=cos2x��ͼ�� ��
��ͼ���Խ�����y=cos2x��ͼ�� ��
A.����ƽ�� ![]() ����λ����
�������
B.����ƽ�� ![]() ����λ����
�������
C.����ƽ�� ![]() ����λ����
�������
D.����ƽ�� ![]() ����λ����
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȲ�����{an}�У�a1=1��ǰn���Sn�������� ![]() =4��n=1��2����
=4��n=1��2����
��1��������{an}��ͨ�ʽ��Sn��
��2����bn= ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڸ߶��꼶����ѡ�Σ�������ѧѡ�ο��������࣮ѡ�ν�����������ѡ��Ӣ���ͬѧҪ�������ѧ������ѧѡ��ÿ��������ٽ�������ͬѧ����ô���ź�������ͬѧ�ķ����У� ��
A.72��
B.54��
C.36��
D.18��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com