
分析 (1)由题意可知,右焦点在圆上或在圆的外部,因此c≥b.即c2≥b2=a2-c2,解出即可得出.
(2)依题意,设直线l:$y=\frac{{\sqrt{3}}}{3}({x-c})$,由l与圆x2+y2=b2相切得$\frac{{|{\frac{{\sqrt{3}}}{3}c}|}}{{\sqrt{1+{{({\frac{{\sqrt{3}}}{3}})}^2}}}}=b$,化简即可得出.
(3)设原点关于直线l对称的点为M(x,y),则M到原点的距离为2b,M到焦点F(c,0)的距离为c.由$\left\{{\begin{array}{l}{{x^2}+{y^2}={{({2b})}^2}}\\{{{({x-c})}^2}+{y^2}={c^2}}\end{array}}\right.$,解出代入椭圆方程解出离心率,比较即可判断出结论.
解答 解:(1)由题意可知,右焦点在圆上或在圆的外部,因此c≥b.
∴c2≥b2=a2-c2,也即$\frac{c^2}{a^2}≥\frac{1}{2}$,解之可得$\frac{{\sqrt{2}}}{2}≤e<1$.
∴椭圆的离心率e的取值范围是$[{\frac{{\sqrt{2}}}{2},1})$.
(2)依题意,设直线l:$y=\frac{{\sqrt{3}}}{3}({x-c})$,由l与圆x2+y2=b2相切得$\frac{{|{\frac{{\sqrt{3}}}{3}c}|}}{{\sqrt{1+{{({\frac{{\sqrt{3}}}{3}})}^2}}}}=b$,即c2=4b2,
∴c2=4(a2-c2),解得$e=\frac{{2\sqrt{5}}}{5}$.
(3)设原点关于直线l对称的点为M(x,y),则M到原点的距离为2b,M到焦点F(c,0)的距离为c.
由$\left\{{\begin{array}{l}{{x^2}+{y^2}={{({2b})}^2}}\\{{{({x-c})}^2}+{y^2}={c^2}}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{x={{\frac{2b}{c}}^2}}\\{{y^2}=\frac{{4{b^2}{c^2}-4{b^4}}}{c^2}}\end{array}}\right.$,代入椭圆方程可得4b2=3a2,易得$e=\frac{1}{2}$
这与$\frac{{\sqrt{2}}}{2}≤e<1$矛盾,故离心率不存在.
点评 本题考查了椭圆底边在方程及其性质、直线与圆相切的性质、点到直线的距离公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 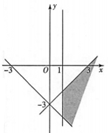 | B. | 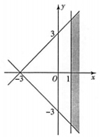 | C. | 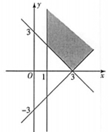 | D. | 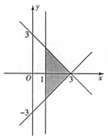 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
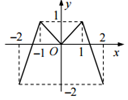 如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )
如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
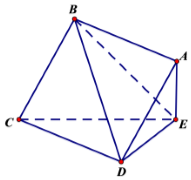 如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com