
 ij��������Ϊ���˽�˿�ʹ�����Ƴ���ij���│�Ĺ˿͵�����ֲ���������������100λ���������Ĺ���Ĺ˿����䣬��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������������[55��65����[65��75����[75��85]�ڵ�Ƶ��֮��Ϊ4��2��1��
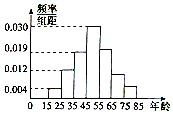
ij��������Ϊ���˽�˿�ʹ�����Ƴ���ij���│�Ĺ˿͵�����ֲ���������������100λ���������Ĺ���Ĺ˿����䣬��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������������[55��65����[65��75����[75��85]�ڵ�Ƶ��֮��Ϊ4��2��1������ ��1������Ƶ�ʺ�Ϊ1�������������[75��85]�ڵ�Ƶ��ֵ��
��2�������������[55��65����[65��75���зֱ��ȡ�������������оٷ���������¼����������Ӧ�ĸ���ֵ��
��� �⣺��1��������[75��85]�ڵ�Ƶ��Ϊx���� ����[55��65����[65��75���ڵ�Ƶ�ʷֱ�Ϊ4x��2x��
������ã�0.004+0.012+0.019+0.03����10+4x+2x+x=1��
���x=0.05��
��������[75��85]�ڵ�Ƶ��Ϊ0.05��
��2����������ã����������[55��65����[65��75���зֱ��ȡ4�˺�2�ˣ�
����[55��65����4�˷ֱ�Ϊa��b��c��d����[65��75����2�˷ֱ�Ϊm��n��
������ȡ�Ľ������15�֣�
��a��b������a��c������a��d������a��m������a��n����
��b��c������b��d������b��m������b��n����
��c��d������c��m������c��n����
��d��m������d��n������m��n����
�衰�������ڲ�ͬ�����顱Ϊ�¼�A���¼�A�����Ļ����¼���8�֣�
��a��m������a��n������b��m������b��n����
��c��m������c��n������d��m������d��n����
�� $P��A��=\frac{8}{15}$��
�����������ڲ�ͬ������ĸ���Ϊ$\frac{8}{15}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ���Լ��оٷ���ŵ���͵ĸ������⣬�ǻ�����Ŀ��


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{{4\sqrt{2}}}{9}$ | B�� | $\frac{{4\sqrt{2}}}{9}$ | C�� | $-\frac{7}{9}$ | D�� | $\frac{7}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
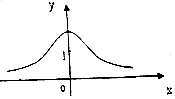 ������R�ϵ�ż����f��x��=$\frac{ax+b}{{x}^{2}+c}$��ͼ����ͼ��ʾ����ʵ��a��b��c�Ĵ�С��ϵ��b��c��a��
������R�ϵ�ż����f��x��=$\frac{ax+b}{{x}^{2}+c}$��ͼ����ͼ��ʾ����ʵ��a��b��c�Ĵ�С��ϵ��b��c��a���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[-\frac{{\sqrt{3}}}{2}��\frac{{\sqrt{3}}}{2}]$ | B�� | $[-\sqrt{3}��\sqrt{3}]$ | C�� | [-2��2] | D�� | [-1��1] |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com