Question

设f（x）是以4为周期的偶函数，且当x∈[0，2]时，f（x）=2^x，则f（log₂15）=    ．

Answer 1

【答案】分析：由f（x）是以4为周期的偶函数，知f（log₂15）=f（log₂15-4）=f（log₂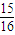），再由当x∈[0，2]时，f（x）=2^x，能求出结果．
解答：解：∵f（x）是以4为周期的偶函数，
且当x∈[0，2]时，f（x）=2^x，
∴f（log₂15）=f（log₂15-4）
=f（log₂15-log₂16）
=f（-log₂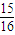）=f（log₂），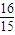
=
=．
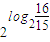
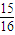
故答案为：．
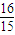
点评：本题考查函数的周期性的应用，是基础题．解题时要认真审题，注意对数性质的灵活运用．