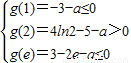设函数f(x)=4lnx-(x-1)2.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)+x2-4x-a=0在区间[1,e]内恰有两个相异的实根,求实数a的取值范围.
【答案】
分析:(I)确定出函数的定义域是解决本题的关键,利用导数作为工具,求出该函数的单调递增区间即为f'(x)>0的x的取值区间;
(II)利用函数思想进行方程根的判定问题是解决本题的关键.构造函数,研究构造函数的性质尤其是单调性,列出该方程有两个相异的实根的不等式组,求出实数a的取值范围.
解答:解:(I)∵函数f(x)=4lnx-(x-1)
2.
∴f′(x)=
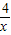
-2x+2=
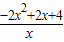
=
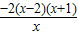
(x>0).
令f′(x)>0,解得x∈(0,2)
故函数f(x)的单调递增区间为(0,2)
(II)关于x的方程f(x)+x
2-4x-a=0
可化为4lnx-(x-1)
2+x
2-4x-a=4lnx-2x-1-a=0
令g(x)=4lnx-2x-1-a
则g′(x)=
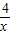
-2
令g′(x)=0,则x=2,
则当0<x<2时,g′(x)>0,g(x)为增函数
当x>2时,g′(x)<0,g(x)为减函数
故当方程f(x)+x
2-4x-a=0在区间[1,e]内恰有两个相异的实根时
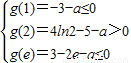
解得3-2e≤a<4ln2-5
故实数a的取值范围为[3-2e,4ln2-5)
点评:本题考查导数的工具作用,考查学生利用导数研究函数的单调性的知识.考查学生对方程、函数、不等式的综合问题的转化与化归思想,将方程的根的问题转化为函数的图象交点问题,属于综合题型.

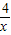 -2x+2=
-2x+2=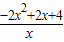 =
=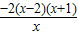 (x>0).
(x>0).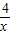 -2
-2