
 ;③正弦函数在第一象限为单调递增函数;④函数y=2sin(2x-
;③正弦函数在第一象限为单调递增函数;④函数y=2sin(2x- )的图象的一个对称点是(
)的图象的一个对称点是( ,0);其中正确命题的序号是 .(把你认为正确命题的序号都填上)
,0);其中正确命题的序号是 .(把你认为正确命题的序号都填上)  ,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;
,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;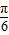 )的图象的对称点坐标为(
)的图象的对称点坐标为(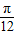 +
+ ,0)(k∈Z),当k=0时为(
,0)(k∈Z),当k=0时为(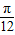 ,0),故④正确;
,0),故④正确;

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
(1)若l垂直于α内两条相交直线,则l⊥α;
(2)若l平行于α,则l平行于α内的所有直线;
(3)若m![]() α,l
α,l![]() β,且l⊥m,则α⊥β;
β,且l⊥m,则α⊥β;
(4)若l![]() β,且l⊥α,则α⊥β;
β,且l⊥α,则α⊥β;
(5)若m![]() α,l
α,l![]() β,且α∥β,则l∥m.
β,且α∥β,则l∥m.
其中正确的命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源:2012-2013年浙江台州六校高二上期中联考理科数学试卷(解析版) 题型:填空题
已知两条不同直线 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
(1)若

 ,
,

 且
且 ∥
∥ ,则
,则 ∥
∥ ;(2)若
;(2)若

 ,
,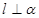 ,则
,则 ⊥
⊥ ;
;
(3)若 ∥
∥ ,则
,则 平行于
平行于 内的所有直线;(4)若
内的所有直线;(4)若 则
则 ⊥
⊥ ;
;
(5)若 在平面
在平面 内的射影互相垂直,则
内的射影互相垂直,则 。
。
其中正确命题的序号是 (把你认为正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三高考极限压轴文科数学试卷(解析版) 题型:填空题
设集合 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质:
(1) ; (2)
; (2) ; (3)
; (3) .
.
给出下列命题:
① :
:
②若 ,则
,则 ;
;
③若 ,且
,且 ,则a = 0;
,则a = 0;
④若, ,且
,且 ,
, ,则a = c.
,则a = c.
其中正确命题的序号是_________ (把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古高三上学期期末文科数学试卷 题型:填空题
设 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 ∥
∥ ;2若
;2若 外的一条直线
外的一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 ∥
∥ ;3设
;3设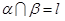 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 ;4直线
;4直线 的充要条件是
的充要条件是 与
与 内的两条直线垂直.其中所有的真命题的序号是
内的两条直线垂直.其中所有的真命题的序号是
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三第二次模拟考试数学试卷 题型:填空题
已知直线m、n,平面 、
、 ,且m⊥
,且m⊥ ,n
,n ,
,
给出下列命题:
①、若 ∥
∥ ,则m⊥n;
,则m⊥n;
②、若m⊥n,则 ∥
∥ ;
;
③、若 ⊥
⊥ ,则m∥n;
,则m∥n;
④、若m∥n,则 ⊥
⊥ .
.
其中正确的命题的序号是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com