
【题目】已知函数![]() 恰有两个零点,则实数
恰有两个零点,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,直线l的参数方程为![]() (t为参数),直线l与曲线C交于M,N两点.
(t为参数),直线l与曲线C交于M,N两点.
(1)若点P的极坐标为(2,π),求|PM||PN|的值;
(2)求曲线C的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保护环境就是保护人类健康.空气中负离子浓度(单位:个/![]() )可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表
)可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表![]() .
.
表![]() 负离子浓度与空气质量对应标准:
负离子浓度与空气质量对应标准:
负离子浓度 | 等级 | 和健康的关系 |
|
| 不利 |
|
| 正常 |
|
| 较有利 |
|
| 有利 |
|
| 相当有利 |
|
| 很有利 |
|
| 极有利 |
图![]() 空气负离子浓度
空气负离子浓度
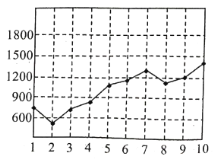
某地连续![]() 天监测了该地空气负离子浓度,并绘制了如图
天监测了该地空气负离子浓度,并绘制了如图![]() 所示的折线图.根据折线图,下列说法错误的是( )
所示的折线图.根据折线图,下列说法错误的是( )
A.这![]() 天的空气负离子浓度总体越来越高
天的空气负离子浓度总体越来越高
B.这![]() 天中空气负离子浓度的中位数约
天中空气负离子浓度的中位数约![]() 个
个![]()
C.后![]() 天的空气质量对身体健康的有利程度明显好于前
天的空气质量对身体健康的有利程度明显好于前![]() 天
天
D.前![]() 天空气质量波动程度小于后
天空气质量波动程度小于后![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】移动支付(支付宝支付,微信支付等)开创了新的支付方式,使电子货币开始普及,为了了解习惯使用移动支付方式是否与年龄有关,对某地200人进行了问卷调查,得到数据如下:60岁以上的人群中,习惯使用移动支付的人数为30人;60岁及以下的人群中,不习惯使用移动支付的人数为40人.已知在全部200人中,随机抽取一人,抽到习惯使用移动支付的人的概率为0.6.
(1)完成如下的列联表,并判断是否有![]() 的把握认为习惯使用移动支付与年龄有关,并说明理由.
的把握认为习惯使用移动支付与年龄有关,并说明理由.
习惯使用移动支付 | 不习惯使用移动支付 | 合计(人数) | |
60岁以上 | |||
60岁及以下 | |||
合计(人数) | 200 |
(2)在习惯使用移动支付的60岁以上的人群中,每月移动支付的金额如下表:
每月支付金额 |
|
|
| 300以上 |
人数 | 10 | 20 |
| 30 |
现采用分层抽样的方法从中抽取9人,再从这9人中随机抽取4人,记4人中每月移动支付金额超过3000元的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin 3x-![]() cos 3x+1的图象向左平移
cos 3x+1的图象向左平移![]() 个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
①它的图象关于直线x=![]() 对称;
对称;
②它的最小正周期为![]() ;
;
③它的图象关于点(![]() ,1)对称;
,1)对称;
④它在[![]() ]上单调递增.
]上单调递增.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com