
【题目】已知一个放置在水平桌面上的密闭直三棱柱![]() 容器,如图1,
容器,如图1,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,里面装有体积为
,里面装有体积为![]() 的液体,现将该棱柱绕
的液体,现将该棱柱绕![]() 旋转至图2.在旋转过程中,以下命题中正确的个数是( )
旋转至图2.在旋转过程中,以下命题中正确的个数是( )

①液面刚好同时经过![]() ,
,![]() ,
,![]() 三点;
三点;
②当平面![]() 与液面成直二面角时,液面与水平桌面的距离为
与液面成直二面角时,液面与水平桌面的距离为![]() ;
;
③当液面与水平桌面的距离为![]() 时,
时,![]() 与液面所成角的正弦值为
与液面所成角的正弦值为![]() .
.
A.0B.1C.2D.3
【答案】D
【解析】
①若液面刚好同时经过![]() ,
,![]() ,
,![]() 三点,则液体的体积为四棱锥
三点,则液体的体积为四棱锥![]() ,进而求解即可;②当平面
,进而求解即可;②当平面![]() 与液面成直二面角时,即为图2的位置,画出图形,可先求得液面上方的三棱柱以四边形为底面的高,再与直三棱柱
与液面成直二面角时,即为图2的位置,画出图形,可先求得液面上方的三棱柱以四边形为底面的高,再与直三棱柱![]() 以四边形为底面的高求差即可;③由①可得此时液面与水平桌面的距离为
以四边形为底面的高求差即可;③由①可得此时液面与水平桌面的距离为![]() ,画出图形,即可求解.
,画出图形,即可求解.
①若液面刚好同时经过![]() ,
,![]() ,
,![]() 三点,则液体的体积为四棱锥
三点,则液体的体积为四棱锥![]() ,
,
因为![]() ,所以①正确;
,所以①正确;
②当平面![]() 与液面成直二面角时,即为图2的位置,设液面与直三棱柱
与液面成直二面角时,即为图2的位置,设液面与直三棱柱![]() 的交点为
的交点为![]() ,如图所示,
,如图所示,
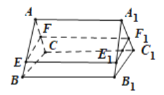
因为直三棱柱![]() 的体积为
的体积为![]() ,
,
所以直棱柱![]() 的体积为
的体积为![]() ,
,
所以![]() ,即
,即![]() ,则在
,则在![]() 中
中![]() 边上的高为
边上的高为![]() ,
,
因为在![]() 中
中![]() 边上的高为
边上的高为![]() ,所以液面与水平桌面的距离为
,所以液面与水平桌面的距离为![]() ,所以②正确;
,所以②正确;
③当液面刚好同时经过![]() ,
,![]() ,
,![]() 三点时,如图所示,
三点时,如图所示,
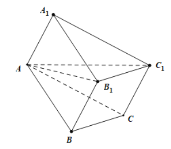
此时![]() ,则
,则![]() ,
,
易得![]() ,则
,则![]() 中
中![]() 边上的高为
边上的高为![]() ,
,
所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,即
,即![]() ,
,
即液面与水平桌面的距离为![]() ,
,
由棱柱的对称性可得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,设
,设![]() 与液面所成角为
与液面所成角为![]() ,
,
则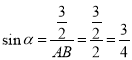 ,所以③正确,
,所以③正确,
所以①②③正确,
故选:D


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业积极响应国家“科技创新”的号召,大力研发人工智能产品,为了对一批新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]()
![]() ,如下表所示:
,如下表所示:
试销单价 | 1 | 2 | 3 | 4 | 5 | 6 |
产品销量 | 91 | 86 |
| 78 | 73 | 70 |
附:参考公式: ,
,![]() ,
,
参考数据:![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)已知变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (百元)的线性回归方程
(百元)的线性回归方程![]() (计算结果精确到整数位);
(计算结果精确到整数位);
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.
时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:

(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的标准长度为![]() ,只要误差的绝对值不超过
,只要误差的绝对值不超过![]() 就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
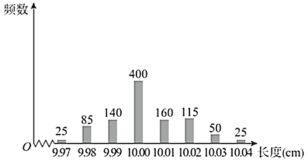
(1)估计该批次产品长度误差绝对值的数学期望;
(2)如果视该批次产品样本的频率为总体的概率,要求从工厂生产的产品中随机抽取2件,假设其中至少有1件是标准长度产品的概率不小于0.8时,该设备符合生产要求.现有设备是否符合此要求?若不符合此要求,求出符合要求时,生产一件产品为标准长度的概率的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com