解(1)由
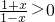
得函数f(x)的定义域为(-1,1)…(2分)
∵
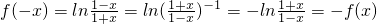
,所以f(x)为奇函数…(4分)
任意x
1,x
2∈(-1,1),x
1<x
2,则
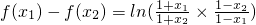
-------------(6分)
∵x
1,x
2∈(-1,1),x
1<x
2,
∴0<1+x
1<1+x
2,0<1-x
2<1-x
1------------(7分)
∴0<
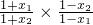
<1,
∴f(x
1)<f(x
2).
所以f(x)为(-1,1)上的递增函数-------------------------------------------------------(9分)
(2)由(1)可知原不等式变形为f(1-m)<f(m
2-1),
又f(x)为(-1,1)上的递增函数,
∴原不等式满足-1<1-m<m
2-1<1,---------------------------------------(11分)
∴m取值范围是
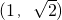
-----------(13分)
分析:(1)由
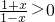
得函数f(x)的定义域;由f(-x)=-f(x)可判断其奇偶性;利用单调性的定义即可证明其单调性;
(2)利用f(x)在x∈(-1,1)上的奇偶性将f(1-m)+f(1-m
2)<0转化为f(1-m)<f(m
2-1),再利用单调性将
函数符号脱掉即可.
点评:本题考查函数奇偶性与单调性的综合,着重考查函数奇偶性的定义与单调性的定义的灵活应用,属于中档题.

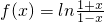 ,
,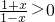 得函数f(x)的定义域为(-1,1)…(2分)
得函数f(x)的定义域为(-1,1)…(2分)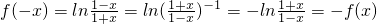 ,所以f(x)为奇函数…(4分)
,所以f(x)为奇函数…(4分)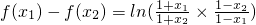 -------------(6分)
-------------(6分)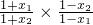 <1,
<1,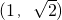 -----------(13分)
-----------(13分)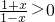 得函数f(x)的定义域;由f(-x)=-f(x)可判断其奇偶性;利用单调性的定义即可证明其单调性;
得函数f(x)的定义域;由f(-x)=-f(x)可判断其奇偶性;利用单调性的定义即可证明其单调性;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案