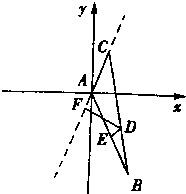
(1)以点A为坐标原点,∠CAB的角平分线所在的直线为x轴,建立平面直角坐标系(如图),设∠CAx=α.
∵
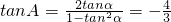
,
∴tanα=2
所以,直线AC的方程为y=2x,直线AB的方程为y=-2x,
双曲线的方程可以设为4x
2-y
2=λ(λ≠0).
设B(x
1,-2x
1),C(x
2,2x
2),由
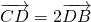
,
得
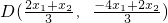
,
所以
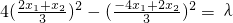
.
即
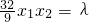
(*)
由
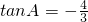
,得
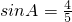
又∵
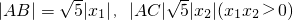
,
∴S
△ABC=
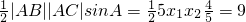
,
即
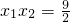
,代入等式(*),得λ=16.
所以,双曲线的方程为
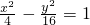
.
(2)由题设可知
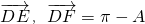
,所以
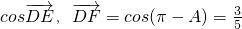
.
设点D(x
0,y
0),
则
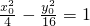
,
于是,点D到AB,AC所在的直线的距离是
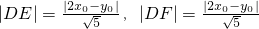
.
故
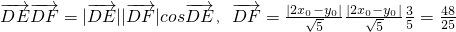
分析:(1)因为以AB,AC所在直线为渐近线,故坐标系必以点A为坐标原点,∠CAB的角平分线所在的直线为一坐标轴.
建系后由
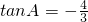
和二倍角公式可写出直线AB,AC的方程,即已知双曲线的渐近线,可将方程设为4x
2-y
2=λ(λ≠0)的形式,再利用双曲线过点D求出λ即可.
(2)设出D点坐标,由点到直线的距离公式求出|DE|,|DF|,再求出DE和DF所成角的余弦值,注意到此角与角A的联系,由向量数量积的定义求解即可.
点评:本题考查求双曲线的方程、双曲线的渐近线等知识,以及平面向量、三角等,综合性较强,考查利用所学知识综合处理问题的能力.

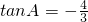 ,且
,且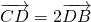 .
.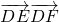 的值.
的值. (1)以点A为坐标原点,∠CAB的角平分线所在的直线为x轴,建立平面直角坐标系(如图),设∠CAx=α.
(1)以点A为坐标原点,∠CAB的角平分线所在的直线为x轴,建立平面直角坐标系(如图),设∠CAx=α.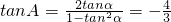 ,
,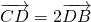 ,
,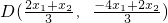 ,
,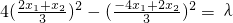 .
.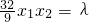 (*)
(*)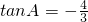 ,得
,得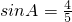 又∵
又∵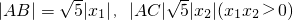 ,
,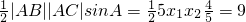 ,
,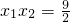 ,代入等式(*),得λ=16.
,代入等式(*),得λ=16.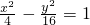 .
.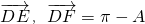 ,所以
,所以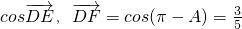 .
.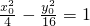 ,
,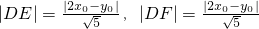 .
.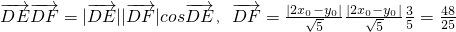
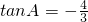 和二倍角公式可写出直线AB,AC的方程,即已知双曲线的渐近线,可将方程设为4x2-y2=λ(λ≠0)的形式,再利用双曲线过点D求出λ即可.
和二倍角公式可写出直线AB,AC的方程,即已知双曲线的渐近线,可将方程设为4x2-y2=λ(λ≠0)的形式,再利用双曲线过点D求出λ即可.

 (2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-
(2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-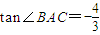 ,且
,且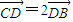 .现建立以A点为坐标原点,以∠BAC的平分线所在直线为x轴的平面直角坐标系,如图所示.
.现建立以A点为坐标原点,以∠BAC的平分线所在直线为x轴的平面直角坐标系,如图所示.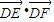 的值.
的值.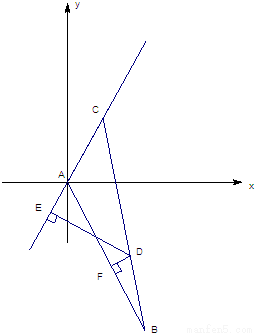
 ,且
,且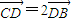 .
.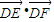 的值.
的值.