
| 1 | 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 解:(Ⅰ)设抛物线的顶点为G(x,y),则其焦点为F(2x-1,y)由抛物线的定义可知:|AF|=点A到直线x=1的距离为2,
解:(Ⅰ)设抛物线的顶点为G(x,y),则其焦点为F(2x-1,y)由抛物线的定义可知:|AF|=点A到直线x=1的距离为2,| 4x2+y2 |
| y2 |
| 4 |
| 1 |
| k |
| 4k2+1 |
| k2 |
| 2bx |
| k |
| 4b 2 |
| k2 |
| 4k2+1 |
| k2 |
| 1 |
| 2 |
| 2bk |
| 4k2+1 |
| 1 |
| 2 |
| 4k2+1 |
| -2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 4 |
3
| ||
| 4 |


科目:高中数学 来源: 题型:
| MB |
| NB |
查看答案和解析>>
科目:高中数学 来源: 题型:
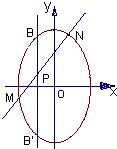
设抛物线过定点A(2, 0), 且以直线![]() 为准线.
为准线.
(1)求抛物线顶点的轨迹C的方程;
(2)已知点B(0, -5), 轨迹C上是否存在满足![]() 的M、N两点?证明你的结论.
的M、N两点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:重庆一模 题型:解答题
| MB |
| NB |
查看答案和解析>>
科目:高中数学 来源:2005年重庆市高考数学一模试卷(文科)(解析版) 题型:解答题
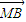 •
•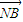 =0的M、N两点?证明你的结论.
=0的M、N两点?证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com