
【题目】设F是椭圆![]() 的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】现有一种水上闯关游戏,共设有3个关口,如果在规定的时间内闯过了这3个关口,那么闯关成功,否则闯关失败,结束游戏.假定小张、小王、小李闯过任何一个关口的概率分别为![]() ,且各关口能否顺利闯过相互独立.
,且各关口能否顺利闯过相互独立.
(1)求小张、小王、小李分别闯关成功的概率;
(2)记小张、小王、小李三人中闯关成功的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点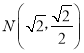 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设V是空间中2019个点构成的集合,其中任意四点不共面某些点之间连有线段,记E为这些线段构成的集合.试求最小的正整数n,满足条件:若E至少有n个元素,则E一定含有908个二元子集,其中每个二元子集中的两条线段有公共端点,且任意两个二元子集的交为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直角梯形
,直角梯形![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三位数中,如果百位数字、十位数字、个位数字刚好能构成等差数列,则称为“等差三位数”,例如:147,642,777,420等等.等差三位数的总个数为( )
A.32B.36C.40D.45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com