Question

【题目】如图，在四棱锥中，平面ABCD，底部ABCD为菱形，E为CD的中点.

（Ⅰ）求证：BD⊥平面PAC；

（Ⅱ）若∠ABC=60°，求证：平面PAB⊥平面PAE；

（Ⅲ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由.

Answer 1

【答案】（Ⅰ）见解析；

（Ⅱ）见解析；

（Ⅲ）见解析.

【解析】

(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；

(Ⅱ)由几何体的空间结构特征首先证得线面垂直，然后利用面面垂直的判断定理可得面面垂直；

(Ⅲ)由题意，利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点.

（Ⅰ）证明：因为平面,所以；

因为底面是菱形，所以;

因为,平面,

所以平面.

（Ⅱ）证明：因为底面是菱形且，所以为正三角形，所以,

因为,所以；

因为平面，平面,

所以；

因为

所以平面，

平面,所以平面平面.

（Ⅲ）存在点为中点时，满足平面；理由如下:

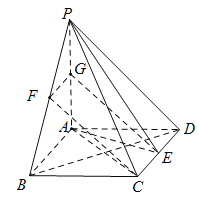
分别取的中点，连接,

在三角形中，且；

在菱形中，为中点，所以且，所以且，即四边形为平行四边形，所以;

又平面，平面，所以平面.