
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,若直线
轴的非负半轴为极轴建立极坐标系,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,过
,过![]() 的直线与直线
的直线与直线![]() 平行,且与曲线
平行,且与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若 ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的个数是( )
①将一组样本数据中的每个数据都加上同一个常数后,方差不变;
②命题![]() ,
,![]() ,命题
,命题![]() ,
,![]() ,则
,则![]() 为真命题;
为真命题;
③“![]() ”是“
”是“![]() 的必要而不充分条件;
的必要而不充分条件;
④将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象.
的图象.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某球员是当今![]() 国内最好的球员之一,在
国内最好的球员之一,在![]() 赛季常规赛中,场均得分达
赛季常规赛中,场均得分达![]() 分。
分。![]() 分球和
分球和![]() 分球命中率分别为
分球命中率分别为![]() 和
和![]() ,罚球命中率为
,罚球命中率为![]() .一场
.一场![]() 比赛分为一、二、三、四节,在某场比赛中该球员每节出手投
比赛分为一、二、三、四节,在某场比赛中该球员每节出手投![]() 分的次数分别是
分的次数分别是![]() ,
,![]() ,
,![]() ,
,![]() ,每节出手投三分的次数分别是
,每节出手投三分的次数分别是![]() ,
,![]() ,
,![]() ,
,![]() ,罚球次数分别是
,罚球次数分别是![]() ,
,![]() ,
,![]() ,
,![]() (罚球一次命中记
(罚球一次命中记![]() 分)。
分)。
(1)估计该球员在这场比赛中的得分(精确到整数);
(2)求该球员这场比赛四节都能投中三分球的概率;
(3)设该球员这场比赛中最后一节的得分为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后,再将所得的图象向下平移一个单位长度得到函数
个单位长度后,再将所得的图象向下平移一个单位长度得到函数![]() 的图象,且
的图象,且![]() 的图象与直线
的图象与直线![]() 相邻两个交点的距离为
相邻两个交点的距离为![]() ,若
,若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种海洋生物身体的长度![]() (单位:米)与生长年限
(单位:米)与生长年限![]() (单位:年)满足如下的函数关系:
(单位:年)满足如下的函数关系:![]() .(设该生物出生时
.(设该生物出生时![]() )
)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第![]() 年,该生物长得最快,求
年,该生物长得最快,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班45人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 5 | ||
合计 | 45 |
已知在全部45人中随机抽取1人,是男同学的概率为![]()
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜爱打篮球与性别有关,请说明理由。
的把握认为喜爱打篮球与性别有关,请说明理由。
附参考公式:![]()
| 0.15 | 0,10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快,已知每投放![]() 个(
个(![]() ,且
,且![]() )单位的洗衣液在一定量水的洗衣机中, 它在水中释放的浓度
)单位的洗衣液在一定量水的洗衣机中, 它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中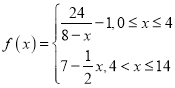 .若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液浓度不低于
.若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液浓度不低于![]() 克/升时,它才能起到有效去污的作用.
克/升时,它才能起到有效去污的作用.
(1)若只投放一次![]() 个单位的洗衣液,当两分钟时水中洗衣液的浓度为
个单位的洗衣液,当两分钟时水中洗衣液的浓度为![]() 克/升,求
克/升,求![]() 的值;
的值;
(2)若只投放一次![]() 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
(3)若第一次投放![]() 个单位的洗衣液,
个单位的洗衣液,![]() 分钟后再投放
分钟后再投放![]() 个单位的洗衣液,则在第
个单位的洗衣液,则在第![]() 分钟时洗衣液是否还能起到有效去污的作用?请说明理由.
分钟时洗衣液是否还能起到有效去污的作用?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com