
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.

(Ⅰ)由折线图得,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系.求
之间的关系.求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 公司2017年5月份(即
公司2017年5月份(即![]() 时)的市场占有率;
时)的市场占有率;

(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的![]() 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不形同,考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表见上表.
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不形同,考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表见上表.
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
(参考公式:回归直线方程为![]() ,其中
,其中![]() )
)
【答案】(1) 线性回归方程为![]() ,
,![]() 公司2017年5月份的市场占有率预计为23% (2) 应该采购
公司2017年5月份的市场占有率预计为23% (2) 应该采购![]() 款单车
款单车
【解析】试题分析:(1)根据折线图及平均数公式可求出![]() 与
与![]() 的值从而可得样本中心点的坐标,从而求可得公式
的值从而可得样本中心点的坐标,从而求可得公式![]() 中所需数据,求出
中所需数据,求出![]() ,再结合样本中心点的性质可得
,再结合样本中心点的性质可得![]() ,进而可得
,进而可得![]() 关于
关于![]() 的回归方程,将
的回归方程,将![]() 代入回归方程即可得结果;(2)根据表格中的数据,算出每辆
代入回归方程即可得结果;(2)根据表格中的数据,算出每辆![]() 款车可使用
款车可使用![]() 年的概率,从而可得每辆
年的概率,从而可得每辆![]() 款车可产生的利润期望值,同理可得每辆
款车可产生的利润期望值,同理可得每辆![]() 款车可产生的利润期望值,比较两期望值的大小即可得出结论.
款车可产生的利润期望值,比较两期望值的大小即可得出结论.
试题解析:(Ⅰ)计算可得![]() ,
,
![]() .
.
![]() .
.![]() 月度市场占有率
月度市场占有率![]() 与月份序号
与月份序号![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
当![]() 时,
时,![]() .故
.故![]() 公司2017年5月份的市场占有率预计为23%.
公司2017年5月份的市场占有率预计为23%.
(Ⅱ)由频率估计概率,每辆![]() 款车可使用1年、2年、3年和4年的概率分别为0.2、0.35、0.35和0.1,
款车可使用1年、2年、3年和4年的概率分别为0.2、0.35、0.35和0.1,![]() 每辆
每辆![]() 款车可产生的利润期望值为
款车可产生的利润期望值为
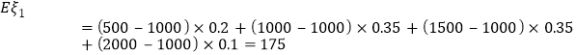 (元).
(元).
频率估计概率,每辆![]() 款车可使用1年、2年、3年和4年的概率分别为0.1、0.3、0.4和0.2,
款车可使用1年、2年、3年和4年的概率分别为0.1、0.3、0.4和0.2,
![]() 每辆
每辆![]() 款车可产生的利润期望值为:
款车可产生的利润期望值为:
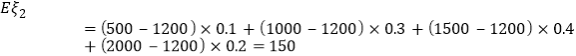 (元),
(元),![]() 应该采购
应该采购![]() 款单车.
款单车.
【方法点晴】本题主要考查折线图的应用与线性回归方程,以及离散型随机变量的分布列与期望,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ; 回归直线过样本点中心
; 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4这五个数字组成无重复数字的自然数.
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β

(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]()
(3)在(2)条件下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com