
【题目】已知直线l的参数方程为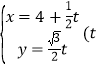 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】偶函数f(x)(x∈R)满足:f(﹣4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为( )
A.(﹣∞,﹣4)∪(4,+∞)
B.(﹣4,﹣1)∪(1,4)
C.(﹣∞,﹣4)∪(﹣1,0)
D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年世界海洋日暨全国海洋宣传日主场活动在海南三亚举行,此次活动主题为“珍惜海洋资源保护海洋生物多样性”,旨在进一步提高公众对节约利用海洋资源.保护海洋生物多样性的认识,为保护蓝色家园做出贡献.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”,为了响应世界海洋日的活动,2019年12月北京某高校行政主管部门从该大学随机抽取部分大学生进行一次海洋知识测试,并根据被测验学生的成绩(得分都在区间![]() 内)绘制成如图所示的频率分布直方图.
内)绘制成如图所示的频率分布直方图.
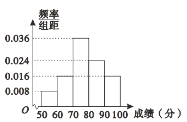
若学生的得分成绩不低于80分的认为是“成绩优秀”现在从认为“成绩优秀”的学生中根据原有分组按照分层抽样的方法抽取10人进行奖励,最后再从这10人中随机选取3人作为优秀代表发言.
(1)求所抽取的3人不属于同一组的概率;
(2)记这3人中,![]() 为测试成绩在
为测试成绩在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)判断函数![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)是否存在实数![]() ,使得当
,使得当![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足
的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足![]() .过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N,则
.过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .现有如下两种图象变换方案:
.现有如下两种图象变换方案:
方案1:将函数![]() 的图像上所有点的横坐标变为原来的一半,纵坐标不变,再将所得图象向左平移
的图像上所有点的横坐标变为原来的一半,纵坐标不变,再将所得图象向左平移![]() 个单位长度;
个单位长度;
方案2:将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再将所得图象上所有点的横坐标变为原来的一半,纵坐标不变.
个单位长度,再将所得图象上所有点的横坐标变为原来的一半,纵坐标不变.
请你从中选择一种方案,确定在此方案下所得函数![]() 的解析式,并解决如下问题:
的解析式,并解决如下问题:
(1)画出函数![]() 在长度为一个周期的闭区间上的图象;
在长度为一个周期的闭区间上的图象;
(2)请你研究函数![]() 的定义域,值域,周期性,奇偶性以及单调性,并写出你的结论.
的定义域,值域,周期性,奇偶性以及单调性,并写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com