
【题目】判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3)x∈{x|x>0}, ![]() ;
;
(4)x0∈Z,log2x0>2.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
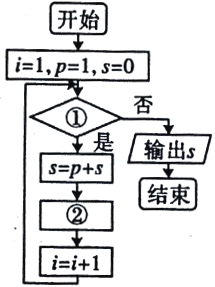
【题目】给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
A. ![]() ;
; ![]() B.
B. ![]() ;
; ![]()
C. ![]() ;
; ![]() D.
D. ![]() ;
; ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax﹣2a2(x∈R).
(1)关于x的不等式f(x)<0的解集为A,且A[﹣1,2],求a的取值范围;
(2)是否存在实数a,使得当x∈R时, ![]() 成立.若存在给出证明,若不存在说明理由.
成立.若存在给出证明,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
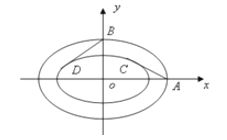
【题目】某奥运会主体育场的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,我们称这两个椭圆相似。
(1)已知椭圆![]() ,写出与椭圆
,写出与椭圆![]() 相似且焦点在
相似且焦点在![]() 轴上、短半轴长为
轴上、短半轴长为![]() 的椭圆
的椭圆![]() 的标准方程;若在椭圆
的标准方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围;
的取值范围;
(2)从外层椭圆顶点A、B向内层椭圆引切线AC、BD,设内层椭圆方程为![]() +
+![]() =1 (a
=1 (a![]() b
b![]() 0),AC与BD的斜率之积为-
0),AC与BD的斜率之积为-![]() ,求椭圆的离心率。
,求椭圆的离心率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com