
分析 (Ⅰ)求出函数的导数,通过解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)(i)求出g(x)的导数,得到关于a,b的方程组,解出即可;
(ii)问题转化为g(x)-k(x2-x)>0对x∈(0,+∞)恒成立.令F(x)=g(x)-k(x2-x),求出函数的导数,通过讨论k的范围,求出函数的单调区间,从而确定k的范围即可.
解答 解:(Ⅰ)当a=1,b=-1时,f(x)=ln(1+x)-x,(x>-1),
则$f'(x)=\frac{1}{1+x}-1=\frac{-x}{1+x}$.
当f'(x)>0时,-1<x<0;
当f'(x)<0时,x>0;
所以f(x)的单调增区间为(-1,0),单调减区间为(0,+∞).…(4分)
(Ⅱ)( i)因为g(x)=f(x)-bx2=ln(1+ax)+b(x-x2),
所以$g'(x)=\frac{a}{1+ax}+b(1-2x)$.
依题设有$\left\{\begin{array}{l}g(1)=ln(1+a)\\ g'(1)=\frac{11}{3}\end{array}\right.$即$\left\{\begin{array}{l}ln(1+a)=ln3\\ \frac{a}{1+a}-b=\frac{11}{3}.\end{array}\right.$
解得$\left\{\begin{array}{l}a=2\\ b=-3\end{array}\right.$.…(8分)
( ii))所以$g(x)=ln(1+2x)-3(x-{x^2}),x∈(-\frac{1}{2},+∞)$.
g(x)>k(x2-x)对x∈(0,+∞)恒成立,
即g(x)-k(x2-x)>0对x∈(0,+∞)恒成立.
令F(x)=g(x)-k(x2-x).
则有$F'(x)=\frac{{4(3-k){x^2}+k-1}}{1+2x}$.
①当1≤k≤3时,当x∈(0,+∞)时,F'(x)>0,
所以F(x)在(0,+∞)上单调递增.
所以F(x)>F(0)=0,即当x∈(0,+∞)时,g(x)>k(x2-x);
②当k<1时,当$x∈(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$时,F'(x)<0,
所以F(x)在$(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$上单调递减,
故当$x∈(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$时,F(x)<F(0)=0,
即当x∈(0,+∞)时,g(x)>k(x2-x)不恒成立.
综上,k∈[1,3]. …(13分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 13 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
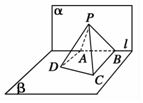 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com