
如图所示棱锥P—ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=![]() ,且PD是四棱锥的高.
,且PD是四棱锥的高.
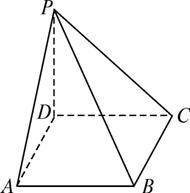
(1)在这个四棱锥中放入一个球,求球的最大半径;
(2)求四棱锥外接球的半径.
(1)球的最大半径为![]() .(2)四棱锥外接球的半径为
.(2)四棱锥外接球的半径为![]() .
.
(1)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连结SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R.
VP—ABCD=![]() ·SABCD·PD=
·SABCD·PD=![]() ·a·a·a=
·a·a·a=![]() a3,
a3,
S△PAD=S△PDC=![]() ·a·a=
·a·a=![]() a2,
a2,
S△PAB=S△PBC=![]() ·a·
·a·![]() =
=![]() ,
,
![]() =a2.
=a2.
VP—ABCD=VS—PDA+VS—PDC+VS—ABCD+VS—PAB+VS—PBC,
![]() R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
![]()
所以![]() ,
,
![]() ,
,
即球的最大半径为![]() .
.
(2)设PB的中点为F.
因为在Rt△PDB中,FP=FB=FD,
在Rt△PAB中,FA=FP=FB,
在Rt△PBC中,FP=FB=FC,
所以FP=FB=FA=FC=FD.
所以F为四棱锥外接球的球心,
则FP为外接球的半径.
因为FB=![]() PB,所以FB=
PB,所以FB=![]() .
.
所以四棱锥外接球的半径为![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•广东)如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且DF=
(2012•广东)如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且DF=| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•哈尔滨一模)如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面 PAD⊥平面ABCD,∠DAB=60°,AB=2且,E为AD 的中点.
(2013•哈尔滨一模)如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面 PAD⊥平面ABCD,∠DAB=60°,AB=2且,E为AD 的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且
(2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com