
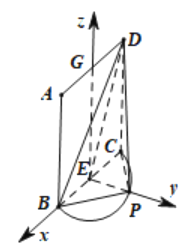
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)利用面面垂直的性质定理证得![]() 平面
平面![]() ,由此证得
,由此证得![]() ,根据圆的几何性质证得
,根据圆的几何性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)判断出三棱锥![]() 的体积最大时
的体积最大时![]() 点的位置.建立空间直角坐标系,通过平面
点的位置.建立空间直角坐标系,通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
(1)证明:因为平面![]() 平面
平面![]() 是正方形,
是正方形,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为点![]() 在以
在以![]() 为直径的半圆弧上,所以
为直径的半圆弧上,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:显然,当点![]() 位于
位于![]() 的中点时,
的中点时,![]() 的面积最大,三棱锥
的面积最大,三棱锥![]() 的体积也最大.
的体积也最大.
不妨设![]() ,记
,记![]() 中点为
中点为![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则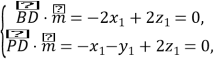 令
令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则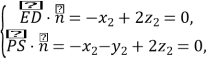 令
令![]() ,得
,得![]() ,
,
所以![]() .
.
由图可知,二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
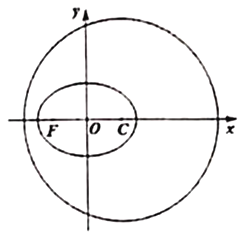
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若直线![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 被椭圆
被椭圆![]() 所截得的弦的长度;
所截得的弦的长度;
(2)若已知点![]() 在椭圆
在椭圆![]() 上,动点
上,动点![]() 满足
满足![]() ,请判断点
,请判断点![]() 与圆
与圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日起新的个人所得税法开始实施,依据《中华人民共和国个人所得税法》可知纳税人实际取得工资、薪金(扣除专项、专项附加及依法确定的其他)所得不超过5000元(俗称“起征点”)的部分不征税,超出5000元部分为全月纳税所得额.新的税率表如下:
2019年1月1日后个人所得税税率表
全月应纳税所得额 | 税率(%) |
不超过3000元的部分 | 3 |
超过3000元至12000元的部分 | 10 |
超过12000元至25000元的部分 | 20 |
超过25000元至35000元的部分 | 25 |
个人所得税专项附加扣除是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息、住房租金和赡养老人等六项专项附加扣除.其中赡养老人一项指纳税人赡养60岁(含)以上父母及其他法定赡养人的赡养支出,可按照以下标准扣除:纳税人为独生子女的,按照每月2000元的标准定额扣除;纳税人为非独生子女的,由其与兄弟姐妹分摊每月2000元的扣除额度,每人分摊的额度不能超过每月1000元.某纳税人为独生子,且仅符合规定中的赡养老人的条件,如果他在2019年10月份应缴纳个人所得税款为390元,那么他当月的工资、薪金税后所得是______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在水平地面上的不同两点处栽有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点![]() 的轨迹可能是( )
的轨迹可能是( )
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上任意一点,直线
上任意一点,直线![]() 与两坐标轴的交点分别为
与两坐标轴的交点分别为![]() ,求
,求![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com