
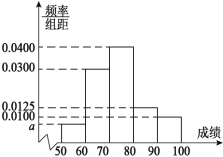
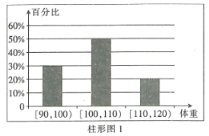
°æƒø°ø÷–π˙‘⁄≈∑÷Þµƒƒ≥ø◊◊”—ß‘∫Œ™¡À»√∏¸∂ýµƒ»À¡ÀΩ‚÷–π˙¥´Õ≥ŒƒªØ£¨‘⁄µ±µÿæŸ∞Ï¡À“ª≥°”…µ±µÿ»À≤Œº”µƒ÷–π˙¥´Õ≥ŒƒªØ÷™ ∂¥Û»¸£¨Œ™¡À¡ÀΩ‚≤Œº”±æ¥Œ¥Û»¸≤Œ»¸»À‘±µƒ≥…º®«Èøˆ£¨¥”≤Œ»¸µƒ»À‘±÷–Àʪ˙≥È»°![]() √˚»À‘±µƒ≥…º®£®¬˙∑÷100∑÷£©◊˜Œ™—˘±æ£¨Ω´À˘µ√ ˝æðΩ¯––∑÷Œˆ’˚¿Ì∫Ûª≠≥ˆ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ 棨“—÷™≥È»°µƒ»À‘±÷–≥…º®‘⁄[50£¨60£©ƒ⁄µƒ∆µ ˝Œ™3.
√˚»À‘±µƒ≥…º®£®¬˙∑÷100∑÷£©◊˜Œ™—˘±æ£¨Ω´À˘µ√ ˝æðΩ¯––∑÷Œˆ’˚¿Ì∫Ûª≠≥ˆ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ 棨“—÷™≥È»°µƒ»À‘±÷–≥…º®‘⁄[50£¨60£©ƒ⁄µƒ∆µ ˝Œ™3.
£®1£©«Û![]() µƒ÷µ∫Õπ¿º∆≤Œ»¸»À‘±µƒ∆Ωæ˘≥…º®£®±£¡Ù–° ˝µ„∫Û¡ΩŒª”––ß ˝◊÷£©£ª
µƒ÷µ∫Õπ¿º∆≤Œ»¸»À‘±µƒ∆Ωæ˘≥…º®£®±£¡Ù–° ˝µ„∫Û¡ΩŒª”––ß ˝◊÷£©£ª
£®2£©“—÷™≥È»°µƒ![]() √˚≤Œ»¸»À‘±÷–£¨≥…º®‘⁄[80£¨90£©∫Õ[90£¨100]≈Æ ø»À ˝∂ºŒ™2»À£¨œ÷¥”≥…º®‘⁄[80£¨90£©∫Õ[90£¨100]µƒ≥È»°µƒ»À‘±÷–∏˜Àʪ˙≥È»°2»À£¨º«’‚4»À÷–≈Æ øµƒ»À ˝Œ™
√˚≤Œ»¸»À‘±÷–£¨≥…º®‘⁄[80£¨90£©∫Õ[90£¨100]≈Æ ø»À ˝∂ºŒ™2»À£¨œ÷¥”≥…º®‘⁄[80£¨90£©∫Õ[90£¨100]µƒ≥È»°µƒ»À‘±÷–∏˜Àʪ˙≥È»°2»À£¨º«’‚4»À÷–≈Æ øµƒ»À ˝Œ™![]() £¨«Û
£¨«Û![]() µƒ∑÷≤º¡–”Î ˝—ß∆⁄Õ˚.
µƒ∑÷≤º¡–”Î ˝—ß∆⁄Õ˚.
°æ¥∞∏°ø£®1£©40£¨73.75£®2£©∑÷≤º¡–º˚Ω‚Œˆ£¨![]()
°æΩ‚Œˆ°ø
£®1£©”…∆µ¬ ∫ÕŒ™1£¨«Û≥ˆ[50£¨60£©µƒ∆µ¬ £¨∆µ ˝Œ™3£¨º¥ø…«Û≥ˆ![]() £¨”…÷±∑ΩÕºΩ·∫œ∆Ωæ˘ ˝π´ Ω£¨º¥ø…«Û≥ˆ∆Ωæ˘ ˝£ª
£¨”…÷±∑ΩÕºΩ·∫œ∆Ωæ˘ ˝π´ Ω£¨º¥ø…«Û≥ˆ∆Ωæ˘ ˝£ª
£®2£©∑÷±«Û≥ˆ≥È»°µƒ»À‘±÷–≥…º®‘⁄[80£¨90£©£¨[90£¨100]µƒ»À ˝£¨![]() µƒø…ƒÐ»°÷µŒ™0£¨1£¨2£¨3£¨4£¨∞¥«Ûπ≈µ‰∏≈–Õ∏≈¬ ∑Ω∑®£¨«Û≥ˆÀʪ˙±‰¡ø
µƒø…ƒÐ»°÷µŒ™0£¨1£¨2£¨3£¨4£¨∞¥«Ûπ≈µ‰∏≈–Õ∏≈¬ ∑Ω∑®£¨«Û≥ˆÀʪ˙±‰¡ø![]() µƒ∏˜∏ˆ÷µµƒ∏≈¬ £¨¡–≥ˆ∑÷≤º¡–£¨º¥ø…«Û≥ˆ ˝—ß∆⁄Õ˚.
µƒ∏˜∏ˆ÷µµƒ∏≈¬ £¨¡–≥ˆ∑÷≤º¡–£¨º¥ø…«Û≥ˆ ˝—ß∆⁄Õ˚.
£®1£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷™£¨≥…º®‘⁄![]() ∆µ¬ Œ™
Ƶ Ϊ
![]() £¨
£¨
![]() ≥…º®‘⁄[50£¨60£©ƒ⁄∆µ ˝Œ™3£¨
≥…º®‘⁄[50£¨60£©ƒ⁄∆µ ˝Œ™3£¨![]() ≥È»°µƒ—˘±æ»ð¡ø
≥È»°µƒ—˘±æ»ð¡ø![]() £¨
£¨
![]() ≤Œ»¸»À‘±∆Ωæ˘≥…º®Œ™
≤Œ»¸»À‘±∆Ωæ˘≥…º®Œ™![]() .
.
£®2£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷™£¨≥È»°µƒ»À‘±÷–≥…º®‘⁄[80£¨90£©µƒ»À ˝Œ™0.0125°¡10°¡40=5£¨
≥…º®‘⁄[90£¨100]µƒ»À ˝Œ™0.0100°¡10°¡40=4£¨
![]() µƒø…ƒÐ»°÷µŒ™0£¨1£¨2£¨3£¨4£¨
µƒø…ƒÐ»°÷µŒ™0£¨1£¨2£¨3£¨4£¨
![]()
![]() £ª
£ª![]()
![]() £¨
£¨
![]()
![]() £¨
£¨![]()
![]() £¨
£¨
![]()
![]() .
.
![]() µƒ∑÷≤º¡–Œ™
µƒ∑÷≤º¡–Œ™
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() .
.


 –¬ÀºŒ¨ºŸ∆⁄◊˜“µ ÓºŸº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
–¬ÀºŒ¨ºŸ∆⁄◊˜“µ ÓºŸº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏ ¿∂ÃÏΩÔ˝ ÓºŸ”≈ªØ—ßœ∞œµ¡–¥∞∏
¿∂ÃÏΩÔ˝ ÓºŸ”≈ªØ—ßœ∞œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄»˝¿‚÷˘ABC©ÅA1B1C1÷–£¨E «¿‚ABµƒ÷–µ„£¨∂ص„F «≤ý√ÊACC1A1£®∞¸¿®±þΩÁ£©…œ“ªµ„£¨»ÙEF//∆Ω√ÊBCC1B1£¨‘Ú∂ص„FµƒπϺ£ «£® £©
A.œþ∂ŒB.‘≤ª°
C.Õ÷‘≤µƒ“ª≤ø∑÷D.≈◊ŒÔœþµƒ“ª≤ø∑÷
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™º´µ„Œ™÷±Ω«◊¯±Íœµµƒ‘≠µ„£¨º´÷·Œ™x÷·’˝∞Î÷·«“µ•Œª≥§∂»œýÕ¨µƒº´◊¯±Íœµ÷–«˙œþ![]() £¨
£¨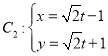 £®tŒ™≤Œ ˝£©.
£®tŒ™≤Œ ˝£©.
£®1£©«Û«˙œþ![]() …œµƒµ„µΩ«˙œþ
…œµƒµ„µΩ«˙œþ![]() æý¿Îµƒ◊Ó–°÷µ£ª
æý¿Îµƒ◊Ó–°÷µ£ª
£®2£©»Ù∞—![]() …œ∏˜µ„µƒ∫·◊¯±Í∂º¿©¥ÛµΩ‘≠¿¥µƒ2±∂£¨◊ð◊¯±Í∂º¿©¥ÛµΩ‘≠¿¥µƒ
…œ∏˜µ„µƒ∫·◊¯±Í∂º¿©¥ÛµΩ‘≠¿¥µƒ2±∂£¨◊ð◊¯±Í∂º¿©¥ÛµΩ‘≠¿¥µƒ![]() ±∂£¨µ√µΩ«˙œþ
±∂£¨µ√µΩ«˙œþ![]() £¨…Ë
£¨…Ë![]() £¨«˙œþ
£¨«˙œþ![]() ”Î
”Î![]() Ωª”⁄A£¨B¡Ωµ„£¨«Û
Ωª”⁄A£¨B¡Ωµ„£¨«Û![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™Õ÷‘≤C£∫![]() (a£æb£æ0)µƒ∂Ã÷·≥§Œ™2£¨F1£¨F2∑÷± «Õ÷‘≤Cµƒ◊Û°¢”“Ω𵄣¨π˝µ„F2µƒ∂Ø÷±œþ”ÎÕ÷‘≤Ωª”⁄µ„P£¨Q£¨π˝µ„F2”ÎPQ¥π÷±µƒ÷±œþ”ÎÕ÷‘≤CΩª”⁄A°¢B¡Ωµ„.µ±÷±œþABπ˝‘≠µ„ ±£¨PF1£Ω3PF2.
(a£æb£æ0)µƒ∂Ã÷·≥§Œ™2£¨F1£¨F2∑÷± «Õ÷‘≤Cµƒ◊Û°¢”“Ω𵄣¨π˝µ„F2µƒ∂Ø÷±œþ”ÎÕ÷‘≤Ωª”⁄µ„P£¨Q£¨π˝µ„F2”ÎPQ¥π÷±µƒ÷±œþ”ÎÕ÷‘≤CΩª”⁄A°¢B¡Ωµ„.µ±÷±œþABπ˝‘≠µ„ ±£¨PF1£Ω3PF2.
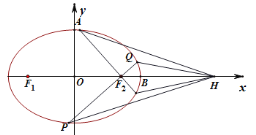
£®1£©«ÛÕ÷‘≤µƒ±Í◊º∑Ω≥ãª
£®2£©»Ùµ„H(3£¨0)£¨º«÷±œþPH£¨QH£¨AH£¨BHµƒ–±¬ “¿¥ŒŒ™![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
¢Ÿ»Ù![]() £¨«Û÷±œþPQµƒ–±¬ £ª
£¨«Û÷±œþPQµƒ–±¬ £ª
¢⁄«Û![]() µƒ◊Ó–°÷µ.
µƒ◊Ó–°÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £Æ
£Æ
£®1£©«Û![]() ‘⁄
‘⁄![]() ¥¶µƒ«–œþ∑Ω≥ã∫
¥¶µƒ«–œþ∑Ω≥ã∫
£®2£©“—÷™ µ ˝![]() ±£¨«Û÷§£∫∫Ø ˝
±£¨«Û÷§£∫∫Ø ˝![]() µƒÕºœÛ”Î÷±œþ
µƒÕºœÛ”Î÷±œþ![]() £∫
£∫![]() ”–3∏ˆΩªµ„£Æ
”–3∏ˆΩªµ„£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
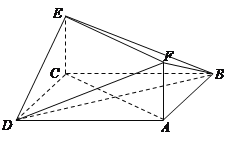
°æƒø°ø‘⁄÷±»˝¿‚÷˘![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨M «≤ý¿‚
£¨M «≤ý¿‚![]() …œ“ªµ„£¨…Ë
…œ“ªµ„£¨…Ë![]() £Æ
£Æ
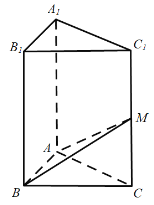
£®1£©»Ù![]() £¨«Û∂ý√ÊÃÂ
£¨«Û∂ý√ÊÃÂ![]() µƒÃª˝£ª
µƒÃª˝£ª
£®2£©»Ù“Ï√Ê÷±œþBM”Î![]() À˘≥…µƒΩ«Œ™
À˘≥…µƒΩ«Œ™![]() £¨«Ûhµƒ÷µ£Æ
£¨«Ûhµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À¡ÀΩ‚‘À∂ØΩ°…̺ı∑ µƒ–ßπ˚£¨ƒ≥Ω°…Ì∑øµ˜≤È¡À20√˚∑ ≈÷’þ£¨Ω°…Ì÷Æ«∞À˚√«µƒÃÂ÷ÿ(µ•Œª£∫![]() )«Èøˆ»Á÷˘–ŒÕº1À˘ 棨æ≠π˝Àƒ∏ˆ‘¬µƒΩ°…Ì∫Û£¨À˚√«µƒÃÂ÷ÿ«Èøˆ»Á÷˘–ŒÕº2À˘ æ.∂‘±»Ω°…Ì«∞∫Û£¨πÿ”⁄’‚20√˚∑ ≈÷’þ£¨œ¬√ÊΩ·¬€’˝»∑µƒ «£® £©
)«Èøˆ»Á÷˘–ŒÕº1À˘ 棨æ≠π˝Àƒ∏ˆ‘¬µƒΩ°…Ì∫Û£¨À˚√«µƒÃÂ÷ÿ«Èøˆ»Á÷˘–ŒÕº2À˘ æ.∂‘±»Ω°…Ì«∞∫Û£¨πÿ”⁄’‚20√˚∑ ≈÷’þ£¨œ¬√ÊΩ·¬€’˝»∑µƒ «£® £©
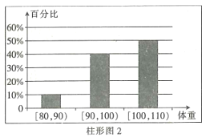
A.À˚√«Ω°…Ì∫Û£¨ÃÂ÷ÿ‘⁄«¯º‰![]() ƒ⁄µƒ»À ˝‘ˆº”¡À2∏ˆ
ƒ⁄µƒ»À ˝‘ˆº”¡À2∏ˆ
B.À˚√«Ω°…Ì∫Û£¨ÃÂ÷ÿ‘⁄«¯º‰![]() ƒ⁄µƒ»À ˝√ª”–∏ƒ±‰
ƒ⁄µƒ»À ˝√ª”–∏ƒ±‰
C.“ÚŒ™ÃÂ÷ÿ‘⁄![]() ƒ⁄À˘’º±»¿˝√ª”–∑¢…˙±‰ªØ£¨À˘“‘Àµ√˜Ω°…Ì∂‘ÃÂ÷ÿ√ª”–»Œ∫Œ”∞œÏ
ƒ⁄À˘’º±»¿˝√ª”–∑¢…˙±‰ªØ£¨À˘“‘Àµ√˜Ω°…Ì∂‘ÃÂ÷ÿ√ª”–»Œ∫Œ”∞œÏ
D.À˚√«Ω°…Ì∫Û£¨‘≠¿¥ÃÂ÷ÿ‘⁄«¯º‰![]() ƒ⁄µƒ∑ ≈÷’þÃÂ÷ÿ∂º”–ºı…Ÿ
ƒ⁄µƒ∑ ≈÷’þÃÂ÷ÿ∂º”–ºı…Ÿ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™’˝∑Ω–ŒABCD∫Õæÿ–ŒACEF÷–£¨AB£Ω![]() £¨CE£Ω1£¨CE°Õ∆Ω√ÊABCD£Æ
£¨CE£Ω1£¨CE°Õ∆Ω√ÊABCD£Æ
£®1£©«Û“Ï√Ê÷±œþDF”ÎBEÀ˘≥…Ω«µƒ”ýœ“÷µ£ª
£®2£©«Û∂˛√ÊΩ«A£≠DF£≠Bµƒ¥Û–°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com