
����Ŀ��Ϊ����ף�л���������![]() ���꣬ij�����ھ��������������ɼ��������ڸ����ѡȡ
���꣬ij�����ھ��������������ɼ��������ڸ����ѡȡ![]() ���������ڵ�λʱ������ͬһ��������������ĺϸ�������ľ�Ҷͼ���£�
���������ڵ�λʱ������ͬһ��������������ĺϸ�������ľ�Ҷͼ���£�
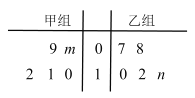
��֪������ѡ���������ĺϸ������ƽ������Ϊ![]() .
.
��1���ֱ����![]() ��ֵ��
��ֵ��
��2���ֱ�����������鼼���ڵ�λʱ���ڼӹ��ĺϸ�����ķ���![]() ��
��![]() ,���ɴ˹������鼼��������ˮƽ��
,���ɴ˹������鼼��������ˮƽ��
��3������λʱ���������ĺϸ����������С��ƽ�����ļ�����Ϊ�������������������������ݣ��ܷ���Ϊ�ó���50%���ϵļ��������������֣�
(ע������![]() ,����
,����![]() ����
Ϊ����![]() ��ƽ����).
��ƽ����).
���𰸡���1��![]() ,
,![]() .��2���𰸼�������3���𰸼�����
.��2���𰸼�������3���𰸼�����
��������
��1������������ѡ���������ĺϸ������ƽ������Ϊ![]() ���������
���������![]() ,
,![]() ��
��
��2�����ݷ��ʽ���������![]() ,
,![]() ,�ɵ�
,�ɵ�![]() ,���ݷ���ĺ��壬����ȷ�������
,���ݷ���ĺ��壬����ȷ�������
��3����Ϊ���鼼����λʱ���������ĺϸ����������С��![]() ����
����![]() ��,�ɵ���Ƶ��Ϊ
��,�ɵ���Ƶ��Ϊ![]() ���������⣬����������.
���������⣬����������.
��1����![]()
�ɵ�![]() ,
,
��![]()
�ɵ�![]() ,
,
![]()
![]() ,
,![]() .
.
��2����Ϊ![]() ,
,
![]() ,
,
��Ϊ![]() ,
,
���Թ������鼼����ƽ��ˮƽһ��,�����鼼��������ˮƽ���ȶ���Ҫ���������һЩ.
��3����Ϊ���鼼����λʱ���������ĺϸ����������С��![]() ����
����![]() ��,��Ƶ��Ϊ
��,��Ƶ��Ϊ![]() ,
,
���Կ��Թ��Ƹó���![]() ���ϵļ���������������.
���ϵļ���������������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҽ�ƴ�ѧʵϰС��Ϊ�о�ʵϰ����ҹ�²��뻼��ð����֮��Ĺ�ϵ���ֱ��������ź�ijҽԺ��¼��1�·���3�·�ÿ��5�ա�20�յ���ҹ�²��������ð��������������õ�������ϣ�
���� | 1��5�� | 1��20�� | 2��5�� | 2��20�� | 3��5�� | 3��20�� |
��ҹ�²� | 10 | 11 | 13 | 12 | 8 | 6 |
�������� | 22 | 25 | 29 | 26 | 16 | 12 |
��С��ȷ�����о������ǣ��ȴ����������������ѡȡ4�����������Իع鷽�̣�����ʣ���2�����ݽ��м���.
��1����ʣ���2�����ݶ���20�յĸ��ʣ�
��2����ѡȡ����1��20�գ�2��5�գ�2��20�գ�3��5����������.
����������������ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��![]() ��
��![]() �÷�����ʾ����
�÷�����ʾ����
����ij�յ���ҹ�²�Ϊ![]() ��Ԥ��վ�������ԼΪ�����ˣ�
��Ԥ��վ�������ԼΪ�����ˣ�
���ο���ʽ��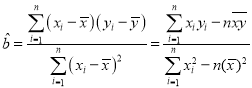 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ������
������![]() .��
.��![]() ��һ��
��һ��![]() ����������
����������![]() ����
����![]() ����
����![]() �Ȳ����溯��Ҳ����ż��������
�Ȳ����溯��Ҳ����ż��������![]() �ĵ�������������
�ĵ�������������![]() ���ݴ��ھ�����
���ݴ��ھ�����![]() ��ֱ���뺯��
��ֱ���뺯��![]() ��ͼ���ཻ.���Ͻ�����ȷ����________________.��д��������ȷ���۵���ţ�
��ͼ���ཻ.���Ͻ�����ȷ����________________.��д��������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ����������ָ��ֱ�Ϊx, y, z, ���ۺ�ָ��S =" x" + y + z���۸ò�Ʒ�ĵȼ�. ��S��4, ��ò�ƷΪһ��Ʒ. �ִ�һ���ò�Ʒ��, �����ȡ10����Ʒ��Ϊ����, ������ָ���б�����:
��Ʒ��� | A1 | A2 | A3 | A4 | A5 |
����ָ��(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
��Ʒ��� | A6 | A7 | A8 | A9 | A10 |
����ָ��(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(��) �����ϱ��ṩ���������ݹ��Ƹ�����Ʒ��һ��Ʒ��;
(��) �ڸ���Ʒ��һ��Ʒ��, �����ȡ������Ʒ,
(1) �ò�Ʒ����г����п��ܵĽ��;
(2) ���¼�BΪ ����ȡ����2����Ʒ��, ÿ����Ʒ���ۺ�ָ��S������4��, ���¼�B�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͶ�ʹ�˾�ƻ�Ͷ��![]() ��
��![]() ���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬
���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬![]() ��Ʒ������
��Ʒ������![]() ��Ͷ����x�������������ϵ��ͼ1��
��Ͷ����x�������������ϵ��ͼ1��![]() ��Ʒ������
��Ʒ������![]() ��Ͷ����x������ƽ�����������������ϵ��ͼ2����������Ͷ������λ����Ԫ��
��Ͷ����x������ƽ�����������������ϵ��ͼ2����������Ͷ������λ����Ԫ��
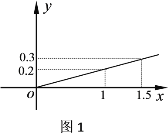
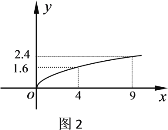
��1���ֱ�![]() ��
��![]() ����Ʒ�������ʾΪͶ�����ĺ�����ϵʽ��
����Ʒ�������ʾΪͶ�����ĺ�����ϵʽ��
��2���ù�˾����20��Ԫ�ʽ𣬲�ȫ��Ͷ��![]() ��
��![]() ���ֲ�Ʒ�У��ʣ�����������20��ԪͶ�ʣ�����ʹ��˾�������������������Ϊ������Ԫ��
���ֲ�Ʒ�У��ʣ�����������20��ԪͶ�ʣ�����ʹ��˾�������������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ϱ���ʱ����ΰ����ѧ���敜����ѧ����ͻ�����ף�����ʵ���Ļ���������敜ԭ���������Ƽ�ͬ�������������.�京���ǣ���������ƽ��ƽ��֮������������壬��ƽ����������ƽ�������ƽ�����أ�����صõ�����������������ȣ���ô������������������ȣ���ͼ����������ƽ��ƽ��֮������������������ֱ�Ϊ![]() ����ƽ����������ƽ�������ƽ��صõ��������������ֱ�Ϊ
����ƽ����������ƽ�������ƽ��صõ��������������ֱ�Ϊ![]() ������
������![]() �����������
�����������![]() ������ģ� ��
������ģ� ��
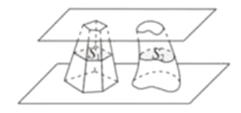
A.��ֲ���Ҫ����B.��Ҫ���������
C.��ֱ�Ҫ����D.�Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
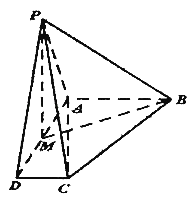
����Ŀ������P��ABCD��ƽ��PAD��ƽ��ABCD��AB��CD��AB��AD��MΪAD�е㣬PA��PD![]() ��AD��AB��2CD��2��
��AD��AB��2CD��2��
��1����֤��ƽ��PMB��ƽ��PAC��
��2��������A��PC��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����Բ
����Բ![]() ��
��![]() �ij���Ϊ���ᣬ��������Բ����������ͬ����OΪ����ԭ�㣬��A��B�ֱ�����Բ
�ij���Ϊ���ᣬ��������Բ����������ͬ����OΪ����ԭ�㣬��A��B�ֱ�����Բ![]() ��
��![]() �ϣ���
�ϣ���![]() ����ֱ��AB��б��kΪ�� ��.
����ֱ��AB��б��kΪ�� ��.
A.1B.-1C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������Ϊ���������˶������ͳ����ijС��100������ƽ��ÿ����˶�ʱ������λ��Сʱ��������ͳ�����ݷ�Ϊ![]() ����С�飨������ľ���ƽ��ÿ���˶�ʱ������
����С�飨������ľ���ƽ��ÿ���˶�ʱ������![]() �ڣ����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
�ڣ����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
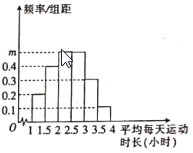
��1�����ͼ��![]() ��ֵ����������
��ֵ����������![]() ������ƽ��ÿ���˶�ʱ����ƽ��ֵ����λ����ͬһ���е�ÿ�����ݿ��ø���������е�ֵ���棩��
������ƽ��ÿ���˶�ʱ����ƽ��ֵ����λ����ͬһ���е�ÿ�����ݿ��ø���������е�ֵ���棩��
��2��Ϊ�˷�������С������ƽ��ÿ����˶�����ְҵ������ȵĹ�ϵ�������Ű�С���÷ֲ�����ķ������20�������һ�����飬������![]() ʱ�����Ӧ��������ˣ�
ʱ�����Ӧ��������ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com