
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | ① | 0.16 |
[70,80) | 22 | ② |
[80,90) | 14 | 0.28 |
[90,100) | ③ | ④ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同.
①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为X,求X的分布列及数学期望.
【答案】
(1)解:根据样本容量,频率和频数之间的关系得到①0.16×50=8② ![]() =0.44
=0.44
③50﹣8﹣22﹣14=6④ ![]() =0.12
=0.12
(2)解:由(1)得,p=0.4,
①该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,
第4道也能够答对才获得一等奖,
则有C31×0.4×0.62×0.4=0.1728.
②答对2道题就终止答题,并获得一等奖,
∴该同学答题个数为2、3、4.
即X=2、3、4,
P(X=2)=0.42=0.16,
P(X=3)=C210.4×0.6×0.4+0.63=0.408,
P(X=4)=C310.4×0.62=0.432,
∴分布列为:
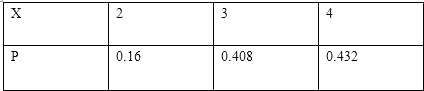
∴EX=2×0.16+3×0.408+4×0.432=3.272.
【解析】(1)由样本容量,频率和频数之间的关系可得序号①、②、③、④的答案; (2)①由相互独立事件的概率公式可得该同学恰好答满4道题而获得一等奖的概率;②先分别求出随机变量的所有可能取值的概率,再写出分布列,进而可得数学期望.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x) 的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx(a为实常数)
(Ⅰ)若a=﹣2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,有2Sn=n2+n+4(n∈+)
(1)求数列的通项公式an;
(2)若bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2a|+|x﹣1|,a∈R.
(1)当a=1时,解不等式f(x)≤5;
(2)若f(x)≥2对于x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有两个独立的转盘(![]() )、(
)、(![]() ).两个图中三个扇形区域的圆心角分别为
).两个图中三个扇形区域的圆心角分别为![]() 、
、![]() 、
、![]() .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(![]() )指针所对的数为
)指针所对的数为![]() ,转盘(
,转盘(![]() )指针所对的数为
)指针所对的数为![]() ,(
,(![]() 、
、![]() ),求下列概率:
),求下列概率:

(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且a1=2,an+1=2Sn+2.
(1)求数列{an}的通项公式;
(2)若数列{bn}的各项均为正数,且bn是 ![]() 与
与 ![]() 的等比中项,求bn的前n项和Tn .
的等比中项,求bn的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com