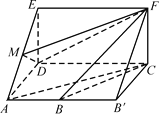
[题目]如图.四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF.∠BAD＝∠CDA＝90°..M是线段AE上的动点．(1)试确定点M的位置.使AC∥平面MDF.并说明理由,(2)在(1)的条件下.求平面MDF将几何体ADE-BCF分成的两部分的体积之比．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD＝∠CDA＝90°，，M是线段AE上的动点．

（1）试确定点M的位置，使AC∥平面MDF，并说明理由；

（2）在（1）的条件下，求平面MDF将几何体ADE－BCF分成的两部分的体积之比．

【答案】（1）见解析

（2）1:4

【解析】（1）当M是线段AE的中点时，AC∥平面MDF．证明如下：

连结CE，交DF于N，连结MN，

由于M、N分别是AE、CE的中点，所以MN∥AC，

由于MN平面MDF，又AC平面MDF，

所以AC∥平面MDF．

（2）如图，将几何体ADE－BCF补成三棱柱ADE－BCF，

三棱柱ADE－BCF的体积为，

则几何体ADE－BCF的体积

＝．

三棱锥F－DEM的体积V三棱锥M－DEF＝，

故两部分的体积之比为（答1:4，4，4:1均可）．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy上取两个定点再取两个动点，，且．

（Ⅰ）求直线与交点M的轨迹C的方程；

（Ⅱ）过的直线与轨迹C交于P,Q，过P作轴且与轨迹C交于另一点N，F为轨迹C的右焦点，若,求证：.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设，曲线在点处的切线与直线垂直．

（1）求的值；

（2）若对于任意的，恒成立，求的取值范围；

（3）求证：．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图, 在△中, 点在边上, .

（Ⅰ）求；

（Ⅱ）若△的面积是, 求.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知曲线y=Asin（ωx+φ）（A＞0，ω＞0）上的一个最高点的坐标为（，），由此点到相邻最低点间的曲线与x轴交于点（π，0），φ∈（﹣，）．

（1）求这条曲线的函数解析式；

（2）写出函数的单调区间．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知长方形ABCD中，AB＝3，AD＝4.现将长方形沿对角线BD折起，使AC＝a，得到一个四面体A－BCD，如图所示.

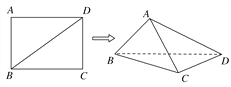
(1)试问：在折叠的过程中，直线AB与CD能否垂直？若能，求出相应a的值；若不能，请说明理由；

(2)求四面体A－BCD体积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点.

求证：(1)平面EFG∥平面ABC；

(2)BC⊥SA.

查看答案和解析>>

科目：高中数学 来源： 题型：

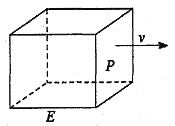
【题目】如图，长方形物体E在雨中沿面P（面积为S）的垂直方向作匀速移动，速度为，雨速沿E移动方向的分速度为。E移动时单位时间内的淋雨量包括两部分：（1）P或P的平行面（只有一个面淋雨）的淋雨量，假设其值与×S成正比，比例系数为；（2）其它面的淋雨量之和，其值为，记为E移动过程中的总淋雨量，当移动距离d=100，面积S=时。