
【题目】如图,在梯形ABCD中,AD//BC,∠ABC=![]() ,
,![]() ,∠ADC=
,∠ADC=![]() ,PA⊥平面ABCD且PA=
,PA⊥平面ABCD且PA=![]() .
.
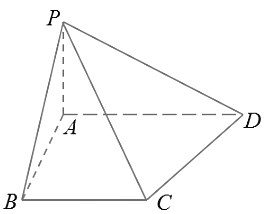
(1)求直线AD到平面PBC的距离;
(2)求出点A到直线PC的距离;
(3)在线段AD上是否存在一点F,使点A到平面PCF的距离为![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)存在,证明见解析.
(3)存在,证明见解析.
【解析】
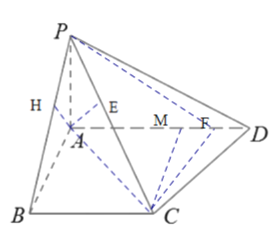
(1)直线AD到平面PBC的距离可转化为点A到平面PBC的距离,作![]() 于
于![]() ,可证明AH的长为点A到平面PBC的距离,求解即可(2)作
,可证明AH的长为点A到平面PBC的距离,求解即可(2)作![]() 于
于![]() ,则AE的长即为点A到PC的距离,利用三角形面积的等积法即可求解(3)假设存在点F,由(2)知只需
,则AE的长即为点A到PC的距离,利用三角形面积的等积法即可求解(3)假设存在点F,由(2)知只需![]() 平面
平面![]() ,转化为是否存在
,转化为是否存在![]() 即可求解.
即可求解.
(1) 作![]() 于
于![]() ,
,
由![]() 面ABCD,
面ABCD,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面PAB,
平面PAB,
![]() ,又
,又![]() ,
,
![]() 面PBC,
面PBC,
即AH的长为点A到平面PBC的距离,也即直线AD到平面PBC的距离,
在等腰![]() 中,
中,![]() ,
,
所以直线AD到平面PBC的距离为![]() .
.
(2)作![]() 于
于![]() ,则AE的长即为点A到PC的距离.
,则AE的长即为点A到PC的距离.
在![]() 中,
中, ![]() ,
,
![]() ,
,
![]()
即点A到直线PC的距离为![]() .
.
(3)假设在线段AD上是存在一点F,使点A到平面PCF的距离为![]() ,
,
设![]()
过C作![]() 于M,在
于M,在![]() 中,
中,![]()
![]() ,
,
可得![]() ,
,![]() ,
,
所以![]() ,
,
由(2)知![]() ,若存在F,使得
,若存在F,使得![]() 平面
平面![]() 即可,
即可,
由条件可知,只需![]() ,则
,则![]() 平面
平面![]()
设![]() ,则
,则![]() ,
,
在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
若![]() ,在
,在![]() 中,
中,
![]() ,
,
即![]() ,
,
解得![]() ,
,
即在AD上存在一点F,当![]() 时,
时,
![]() ,
,
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,即点A到平面PCF的距离为
,即点A到平面PCF的距离为![]() ,
,
此时![]() 满足条件.
满足条件.


科目:高中数学 来源: 题型:
【题目】今有9所省级示范学校参加联考,参加人数约5000人,考完后经计算得数学平均分为113分.已知本次联考的成绩服从正态分布,且标准差为12.
(1)计算联考成绩在137分以上的人数.
(2)从所有试卷中任意抽取1份,已知分数不超过123分的概率为0.8.
①求分数低于103分的概率.
②从所有试卷中任意抽取5份,由于试卷数量较大,可以把每份试卷被抽到的概率视为相同,![]() 表示抽到成绩低于103分的试卷的份数,写出
表示抽到成绩低于103分的试卷的份数,写出![]() 的分布列,并求出数学期望
的分布列,并求出数学期望![]() .
.
参考数据:
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,且AD∥BC,AD⊥CD,∠ABC=60°,BC=2AD=2,PC=3,△PAB是正三角形.
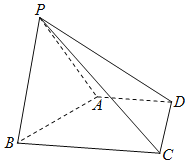
(1)求证:AB⊥PC;
(2)求二面角P﹣CD﹣B的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴的正半轴上,与
轴的正半轴上,与![]() 轴相交于点
轴相交于点![]() ,且直线
,且直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,B(-1,0),C(1,0),AB=6,点P在AB上,且∠BAC=∠PCA.
(1)求点P的轨迹E的方程;
(2)若![]() ,过点C的直线与E交于M,N两点,与直线x=9交于点K,记QM,QN,QK的斜率分别为k1,k2,k3,试探究k1,k2,k3的关系,并证明.
,过点C的直线与E交于M,N两点,与直线x=9交于点K,记QM,QN,QK的斜率分别为k1,k2,k3,试探究k1,k2,k3的关系,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,
内一个定点,![]() 是圆
是圆![]() 上任意-一点,线段
上任意-一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,连接
,连接![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
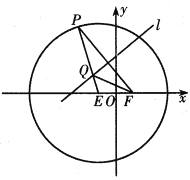
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 、
、![]() 是曲线
是曲线![]() 上关于原点对称的两个点,点
上关于原点对称的两个点,点![]() 是曲线
是曲线![]() .上任意-一点(不同于点
.上任意-一点(不同于点![]() 、
、![]() ),当直线
),当直线![]() 、
、![]() 的斜率都存在时,记它们的斜率分别为
的斜率都存在时,记它们的斜率分别为![]() 、
、![]() ,求证:
,求证:![]() 的为定值.
的为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C顶点在坐标原点,焦点F在Y轴的非负半轴上,点![]() 是抛物线上的一点.
是抛物线上的一点.
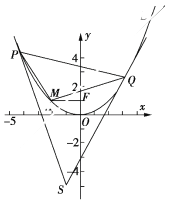
(1)求抛物线C的标准方程
(2)若点P,Q在抛物线C上,且抛物线C在点P,Q处的切线交于点S,记直线 MP,MQ的斜率分别为k1,k2,且满足![]() ,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com