
【题目】在平面四边形ABCD中,AB=8,AD=5,CD=![]() ,∠A=
,∠A=![]() ,∠D=
,∠D=![]() .
.
(Ⅰ)求△ABD的内切圆的半径;
(Ⅱ)求BC的长.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】函数![]() ,其图象与
,其图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,且
两点,且![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)证明: ![]() (
(![]() 为
为![]() 的导函数).
的导函数).
(Ⅲ)设点![]() 在函数
在函数![]() 图象上,且
图象上,且![]() 为等腰直角三角形,记
为等腰直角三角形,记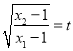 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]()
![]() ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个命题:
(1)函数![]() 内单调递增。
内单调递增。
(2)函数![]() 的最小正周期为2
的最小正周期为2![]() 。
。
(3)函数![]() 的图像关于点
的图像关于点![]() 对称。
对称。
(4)函数![]() 的图像关于直线
的图像关于直线![]() 成轴对称。
成轴对称。
(5)把函数![]() 的图象向右平移
的图象向右平移![]() 得到函数
得到函数![]() 的图象。
的图象。
其中真命题的序号是________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(I)若花店一天购进![]() 枝玫瑰花,写出当天的利润
枝玫瑰花,写出当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(II)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各需求量的频率作为各需求量发生的概率.
天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望.
的分布列,数学期望.
(ii)若花店计划一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?只写结论.
枝?只写结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 相交于点
相交于点![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() 平面
平面![]() .
.
(Ⅲ)求三棱锥![]() 的体积的取值范围.
的体积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数集![]() ,其中
,其中![]() ,
, ![]() ,定义向量集
,定义向量集![]() .若对于任意
.若对于任意![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .例如
.例如![]() 具有性质
具有性质![]() .
.
(![]() )若
)若![]() ,且
,且![]() 具有性质
具有性质![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 具有性质
具有性质![]() ,求证:
,求证: ![]() ,且当
,且当![]() 时,
时, ![]() .
.
(![]() )若
)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() (
(![]() 为常数),求有穷数列
为常数),求有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项![]() ,
, ![]() ,
, ![]() .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)记![]() ,若Sn<100,求最大正整数n;
,若Sn<100,求最大正整数n;
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列,且am-1,as-1,an-1成等比数列?如果存在,请给以证明;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com