[题目]已知m＞0.n＞0.x=m+n.y= ．(1)求xy的最小值,(2)若2x+y=15.求x的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知m＞0，n＞0，x=m+n，y= ．
（1）求xy的最小值；
（2）若2x+y=15，求x的取值范围．

【答案】
（1）解：m＞0，n＞0，依题意，xy=（m+n）（）=17+ , ≥17+2 =25，

当且仅当n=4m时“=”成立

（2）解：∵2x+y=15，∴y=15﹣2x，

由（1）得：xy≥25，

∴x（15﹣2x）≥25，

∴2x2﹣15x+25≤0，

∴ ≤x≤5

【解析】（1）应用级别不等式的性质求出其最小值即可；（2）求出y=15﹣2x，由（1）得：xy≥25，消去y解关于x的不等式即可．
【考点精析】利用基本不等式对题目进行判断即可得到答案，需要熟知基本不等式：,（当且仅当时取到等号）；变形公式：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直，M，Q分别为PC，AD的中点．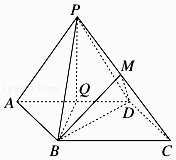
（1）求证：PA∥平面MBD；
（2）求二面角P﹣BD﹣A的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知关于x，y的方程C：x2+y2﹣2x﹣4y+m=0
（1）当方程C表示圆时，求m的取值范围；
（2）若圆C与直线l1：x+2y﹣4=0相交于M，N两点，且|MN|= ，求m的值；
（3）在（2）条件下，若圆C上存在四点到直线l2：x﹣2y+b=0的距离均为，试求b的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，记正方形ABCD四条边的中点为S，M，N，T，连接四个中点得小正方形SMNT．将正方形ABCD，正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1 ， V2 ，则V1：V2=（）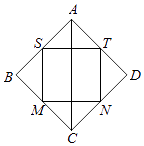

A.8：1
B.2：1
C.4：3
D.8：3

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱柱A1B1C1﹣A2B2C2中，各侧棱均垂直于底面，∠A1B1C1=90°，A1B1=B1C1=3，C1M=2B1N=2，则直线B1C1与平面A1MN所成角的正弦值为．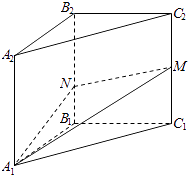

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）= x﹣lnx（x＞0），则函数f（x）（）
A.在区间（0，1）内有零点，在区间（1，+∞）内无零点
B.在区间（0，1）内有零点，在区间（1，+∞）内有零点
C.在区间（0，3），（3，+∞）均无零点
D.在区间（0，3），（3，+∞）均有零点

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一个工厂生产某种产品每年需要固定投资万元，此外每生产件该产品还需要增加投资万元，年产量为件．当时，年销售总收入为万元；当时，年销售总收入为万元．记该工厂生产并销售这种产品所得的年利润为万元。
（1）求（万元）关于（件）的函数关系式；
（2）该工厂的年产量为多少件时，所得年利润最大？并求出最大值．（年利润＝年销售总收入年总投资）