
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(Ⅰ)若![]() 为
为![]() 的极值点,求实数
的极值点,求实数![]() 的取值范围.
的取值范围.
(Ⅱ)讨论函数![]() 在
在![]() 上的单调性.
上的单调性.
(Ⅲ)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(1) ![]() ,由题,
,由题, ![]() 为
为![]() 的极值点,
的极值点,
可得![]() ,即
,即![]() .
.
(2) ![]() ,
, ![]() ,分
,分![]() ,
, ![]() ,
, ![]() 三种情况讨论函数的单调性即可.
三种情况讨论函数的单调性即可.
(3)结合(2)的单调性,分别求![]() 和
和![]() 以及
以及![]() 时a的范围,综合取并集可得.
时a的范围,综合取并集可得.
试题解析:(Ⅰ) ![]() ,
,
∵![]() 为
为![]() 的极值点,
的极值点,
∴![]() ,
, ![]() .
.
(Ⅱ)∵![]() ,
, ![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,
,
此时, ![]() 在
在![]() 上单调增,
上单调增,
当![]() 即
即![]() 时,
时, ![]() 时,
时,
![]() ,
, ![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 即
即![]() 时,
时, ![]() ,
, ![]() ,
,
此时, ![]() 在
在![]() 上单调递减.
上单调递减.
(Ⅲ)当![]() 时,∵
时,∵![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 的最小值为
的最小值为![]() ,
,
∴![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 的最小值为
的最小值为![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() .
.
当![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 的最小值为
的最小值为![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
综上可得: ![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需要看不同类型的书籍,为了合理配备资源,现对小区看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图,问:
后得到如图所示的频率分布直方图,问:
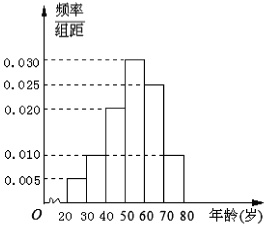
(1)在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)估计40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A. 若![]() 的观测值为
的观测值为![]() ,在犯错误的概率不超过
,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B. 由独立性检验可知,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有![]() 的可能患有肺癌.
的可能患有肺癌.
C. 若从统计量中求出在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D. 以上三种说法都不正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 (
(![]() 是参数)和定点
是参数)和定点![]() ,
,![]() 、
、![]() 是圆锥曲线的左、右焦点.
是圆锥曲线的左、右焦点.
(1)求经过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面A1B1C1D1相交于直线l.

(1)画出直线l的位置,并简单指出作图依据;
(2)设l∩A1B1=P,求线段PB1的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com