
【题目】屠呦呦,第一位获得诺贝尔科学奖项的中国本土科学家,在2015年获得诺贝尔生理学或医学奖,理由是她发现了青蒿素.这种药品可以有效降低疟疾患者的死亡率,从青篙中提取的青篙素抗疟性超强,几乎达到100%.据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
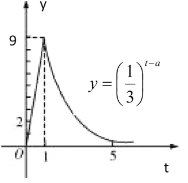
(Ⅰ)写出服药一次后y与t之间的函数关系式![]() ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有3个红球和7个白球,这些球除颜色外完全相同,一次从中摸出3个球.
(1)设![]() 表示摸出的红球的个数,求
表示摸出的红球的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)为了提高同学们参与游戏的积极性,参加游戏的同学每人可摸球两次,每次摸球后放回,若规定两次共摸出红球的个数不少于![]() ,且中奖概率大于60%时,即中奖,求
,且中奖概率大于60%时,即中奖,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 设![]() ,则
,则![]() 为实数的充要条件是
为实数的充要条件是![]() 为共轭复数;
为共轭复数;
B. “直线![]() 与曲线C相切”是“直线
与曲线C相切”是“直线![]() 与曲线C只有一个公共点”的充分不必要条件;
与曲线C只有一个公共点”的充分不必要条件;
C. “若两直线![]() ,则它们的斜率之积等于
,则它们的斜率之积等于![]() ”的逆命题;
”的逆命题;
D. ![]() 是R上的可导函数,“若
是R上的可导函数,“若![]() 是
是![]() 的极值点,则
的极值点,则![]() ”的否命题.
”的否命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图。
分组 | 频数 | 频率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合计 | 1.00 |
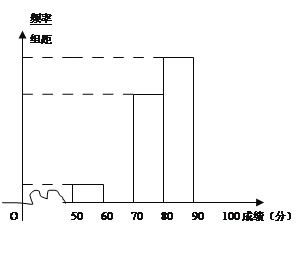
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)请你估算学生成绩的平均数及中位数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com