
已知函数
⑴若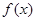 的定义域和值域均是
的定义域和值域均是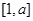 ,求实数
,求实数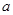 的值;
的值;
⑵若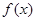 在
在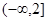 上是减函数,且对任意的
上是减函数,且对任意的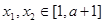 ,总有
,总有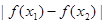 ≤
≤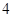 ,求实数
,求实数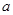 的取值范围.
的取值范围.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=x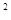 +2ax+2, x
+2ax+2, x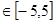 .
.
(1)当a=-1时,求函数的最大值和最小值;
(2) 若y=f(x)在区间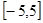 上是单调 函数,求实数 a的取值范围.
上是单调 函数,求实数 a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①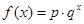 ;②
;②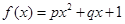 ;③
;③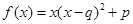 .(以上三式中、
.(以上三式中、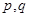 均为常数,且
均为常数,且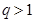 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(II)若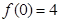 ,
,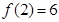 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是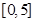 .其中
.其中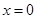 表示8月1日,
表示8月1日,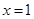 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)在(II)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保护水资源,提倡节约用水,某市对居民生活用水收费标准如下:每户每月用水不超过6吨时每吨3元,当用水超过6吨但不超过15吨时,超过部分每吨5元,当用水超过15吨时,超过部分每吨10元。
(1)求水费y(元)关于用水量x(吨)之间的函数关系式;
(2)若某户居民某月所交水费为93元,试求此用户该月的用水量。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数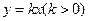 的图象与函数
的图象与函数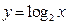 的图象交于两点
的图象交于两点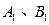 (
(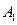 在线段
在线段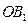 上,
上,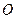 为坐标原点),过
为坐标原点),过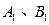 作
作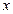 轴的垂线,垂足分别为
轴的垂线,垂足分别为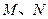 ,并且
,并且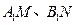 分别交函数
分别交函数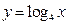 的图象于
的图象于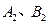 两点.
两点.
(1)试探究线段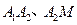 的大小关系;
的大小关系;
(2)若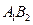 平行于
平行于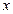 轴,求四边形
轴,求四边形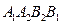 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化工企业2010年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(Ⅰ)求该企业使用该设备x年的年平均污水处理费用y(万元);
(Ⅱ)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.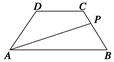
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com