
【题目】已知抛物线![]() ,其中
,其中![]() .点
.点![]() 在
在![]() 的焦点
的焦点![]() 的右侧,且
的右侧,且![]() 到
到![]() 的准线的距离是
的准线的距离是![]() 与
与![]() 距离的3倍.经过点
距离的3倍.经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的方程和![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)![]() ,
,![]() ;(2)平行.
;(2)平行.
【解析】
(1)由![]() 到
到![]() 的准线的距离是
的准线的距离是![]() 与
与![]() 距离的3倍可得p值,从而得到抛物线的方程和
距离的3倍可得p值,从而得到抛物线的方程和![]() 的坐标;
的坐标;
(2)方法一:设直线![]() 的方程为
的方程为![]() ,对m分类讨论,分别计算二者的斜率,即可作出判断.方法二:先考虑直线
,对m分类讨论,分别计算二者的斜率,即可作出判断.方法二:先考虑直线![]() 的斜率不存在时,在考虑直线
的斜率不存在时,在考虑直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立求点坐标,利用两点斜率公式求出
,联立求点坐标,利用两点斜率公式求出![]() ,即可得出结论.
,即可得出结论.
(1)抛物线![]() 的准线方程为
的准线方程为![]() ,焦点坐标为
,焦点坐标为![]() ,
,
所以有![]() ,解得
,解得![]() ,
,
所以抛物线方程为![]() ,焦点坐标为
,焦点坐标为![]() .
.
(2)直线![]() ,
,
方法一:
设![]() ,
,![]() ,
,
设直线![]() 的方程为
的方程为![]()
联立方程 ![]()
消元得,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
显然![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ,则
,则![]()
① 当![]() 时,直线
时,直线![]() 的斜率不存在,
的斜率不存在,![]() ,可知 ,
,可知 ,
直线![]() 的斜率不存在,则
的斜率不存在,则![]()
② 当![]() 时,
时,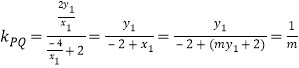 ,
,![]() ,
,
则![]()
综上所述,![]()
方法二:
直线![]()
(i) 若直线![]() 的斜率不存在,根据对称性,不妨设
的斜率不存在,根据对称性,不妨设![]() ,
,![]()
直线![]() 的方程为
的方程为![]() ,则
,则![]()
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,则直线
,则直线![]() 的斜率不存在,因此
的斜率不存在,因此![]()
(ii) 设![]() ,
,![]() ,
,
当直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,![]()
联立方程,![]()
消元得,![]() ,
,
整理得,![]()
由韦达定理,可得![]() ,
,![]()
![]() ,因为
,因为![]() ,可得
,可得![]() .
.
显然![]() ,
,
直线![]() 的方程为
的方程为![]()
令![]() ,则
,则![]() ,则
,则![]()
因为![]() ,所以
,所以![]()
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ,则
,则![]()
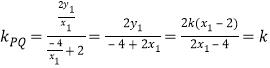 ,则
,则![]()
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(填序号)
①已知![]() 或
或![]() ,
,![]() ,则p是q的充分不必要条件;
,则p是q的充分不必要条件;
②“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 中,内角A,B,C所对的边分别为a,b,c,
中,内角A,B,C所对的边分别为a,b,c,![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() 为等腰三角形”的必要不充分条件;
为等腰三角形”的必要不充分条件;
④若命题![]() “函数
“函数![]() 的值域为
的值域为![]() ”为真命题,则实数a的取值范围是
”为真命题,则实数a的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图1,是某设计员为一种商品设计的平面logo样式.主体是由内而外的三个正方形构成.该图的设计构思如图2,中间正方形![]() 的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为
的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为![]() ,最内正方形
,最内正方形![]() 的面积为
的面积为![]() .当
.当![]() ,且
,且![]() 取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了.卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的42%来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
造林方式 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重庆 | 226333 | 100600 | 62400 | 63333 | ||
陕西 | 297642 | 33602 | 63865 | 16067 | ||
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(I)请根据上述数据分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(Ⅱ)在这十个地区中,任选一个地区,求该地区人工造林面积占造林总面积的比值超过![]() 的概率是多少?
的概率是多少?
(Ⅲ)在这十个地区中,从新封山育林面积超过五万公顷的地区中,任选两个地区,记X为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差
的公差![]() ,数列
,数列![]() 满足
满足![]() ,集合
,集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() ,求
,求![]() 使得集合
使得集合![]() 恰好有两个元素;
恰好有两个元素;
(3)若集合![]() 恰好有三个元素:
恰好有三个元素:![]() ,
,![]() 是不超过7的正整数,求
是不超过7的正整数,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
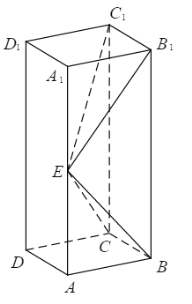
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com