
【题目】如图,已知四棱锥![]() ,
,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
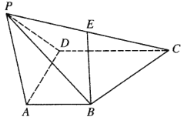
(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
(Ⅰ)先证明![]() 与平面
与平面![]() 中的一条线平行,再应用线面平行的判定定理即可证得结果;
中的一条线平行,再应用线面平行的判定定理即可证得结果;
(Ⅱ)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,由此可推出
,由此可推出![]() 为点
为点![]() 到平面
到平面![]() 的距离,然后通过解直角三角形求解即可.
的距离,然后通过解直角三角形求解即可.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
所以![]() 且
且![]() ,
,
又![]() 且
且![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
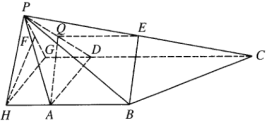
(Ⅱ)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
得![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
由![]() 知,点
知,点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ,
,
设![]() ,则由
,则由![]() 知
知![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则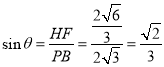 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】培养某种水生植物需要定期向培养植物的水中加入物质![]() ,已知向水中每投放1个单位的物质
,已知向水中每投放1个单位的物质![]() ,
,![]() (单位:天)时刻后水中含有物质
(单位:天)时刻后水中含有物质![]() 的量增加
的量增加![]() ,
,![]() 与
与![]() 的函数关系可近似地表示为关系可近似地表示为
的函数关系可近似地表示为关系可近似地表示为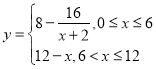 .根据经验,当水中含有物质
.根据经验,当水中含有物质![]() 的量不低
的量不低![]() 时,物质
时,物质![]() 才能有效发挥作用.
才能有效发挥作用.
(1)若在水中首次投放1个单位的物质![]() ,计算物质
,计算物质![]() 能持续有效发挥作用几天?
能持续有效发挥作用几天?
(2)若在水中首次投放1个单位的物质![]() ,第8天再投放1个单位的物质
,第8天再投放1个单位的物质![]() ,试判断第8天至第12天,水中所含物质
,试判断第8天至第12天,水中所含物质![]() 的量是否始终不超过
的量是否始终不超过![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为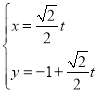 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
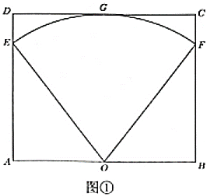
【题目】某公园计划在矩形空地上建造一个扇形花园如图①所示,矩形![]() 的
的![]() 边与
边与![]() 边的长分别为48米与40米,扇形的圆心
边的长分别为48米与40米,扇形的圆心![]() 为
为![]() 中点,扇形的圆弧端点
中点,扇形的圆弧端点![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上,圆弧的中点
上,圆弧的中点![]() 在
在![]() 上.
上.
(1)求扇形花园的面积(精确到1平方米);
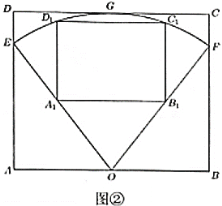
(2)若在扇形花园内开辟出一个矩形区域![]() 为花卉展览区.如图②所示,矩形
为花卉展览区.如图②所示,矩形![]() 的四条边与矩形
的四条边与矩形![]() 的对应边平行,点
的对应边平行,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,点
上,点![]() ,
,![]() 在扇形的弧上.某同学猜想:当矩形
在扇形的弧上.某同学猜想:当矩形![]() 面积最大时,两矩形
面积最大时,两矩形![]() 与
与![]() 的形状恰好相同(即长与宽之比相同),试求花卉展览区
的形状恰好相同(即长与宽之比相同),试求花卉展览区![]() 面积的最大值,并判断上述猜想是否正确(请说明理由).
面积的最大值,并判断上述猜想是否正确(请说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.数列
上.数列![]() 中,点
中,点![]() 在经过点
在经过点![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)对任意的正整数![]() ,不等式
,不等式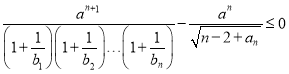 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一种赛车跑道类似“梨形”曲线,由圆弧![]() 和线段AB,CD四部分组成,在极坐标系Ox中,A(2,
和线段AB,CD四部分组成,在极坐标系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圆的圆心分别是(0,0),(2,0),曲线M1是弧
所在圆的圆心分别是(0,0),(2,0),曲线M1是弧![]() ,曲线M2是弧
,曲线M2是弧![]() .
.
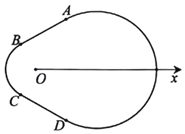
(1)分别写出M1,M2的极坐标方程:
(2)点E,F位于曲线M2上,且![]() ,求△EOF面积的取值范围.
,求△EOF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥底面ABCD,E在PB上.
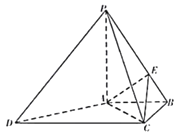
(1)证明:AC⊥PD;
(2)若PE=2BE,求三棱锥P﹣ACE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com